а измерения скорости
движения жидкости.
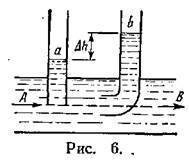
Представим, что в движущуюся жидкость опущены две трубки малого сечения, причем, плоскость поперечного сечения одной из них параллельна направлению скорости движения жидкости v, а другая (трубка Пито) изогнута так, что плоскость сечения изогнутой части
перпендикулярна направлению скорости течения (рис.6). Подъем жидкости в прямой трубке на высоту h1обусловлен лишь статическим давлением Рc, которое можно определить по формуле:
Pc= ρgh1.
В трубке Пито подъем жидкости на высоту h2обусловлен полным давлением Рп- в данном случае суммой статического Рси динамического Рддавлений (течение происходит горизонтально и весовое давление не учитывается). Следовательно:
Рп= Рс+ Рд;
ρgh2 = ρgh1 + ρv2/2
Из последней формулы находим линейную скорость жидкости:
.
Таким образом, по измеренной разности уровней жидкости в прямой и
изогнутой трубках определяется скорость течения жидкости. Этим же
методом определяют и скорость самолета относительно воздуха, катера относительно воды и др.
ответ: v=1,4 М\С
1 задача)Fa=pж*V*g=0,02*0,05*0,1*p(спирта)*10=0,001*p(спирта).
2 задача)
Дано:
Размеры бруска: 5x4x10 см=0,05x0,04x0,1 м.
a=0,05 м.
b=0,04 м.
c=0,1 м.
На 2/3 погружен в керосин.
p=800 кг/м^3. (Плотность керосина).
F(a)=?
Решение:
Формула силы Архимеда:
Где p - плотность керосина, g - ускорение свободного падения, V - объем погруженной части бруска в керосин.
Найдем объем:
V=0,05*0,04*0,1=0,0002 м^3.
Сказано, что в керосин погружено 2/3 от всего объема. Теперь найдем силу Архимеда:
Считаем:
F(a)=(2*800*10*0,0002)/3=1,066 Н.
ответ:F(a)=1,066 Н.
3 задача)Сила тяжести,действующая на оболочку и приборы,равна 40 Н.
Закон Ньтона
4)задача)S=Vl
Fa=роgV