
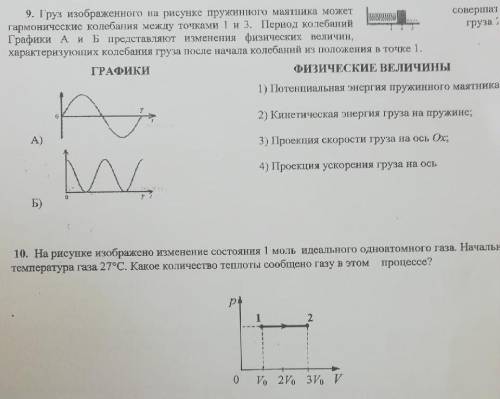
v0 = 3 м/с
а = 2 м/с²
Объяснение:
Мы знаем что
s = v0t + ( at² )/2
или
s = v0t + at²0,5
Зная это составим систему
s(1) = v0t(1) + at(1)²0,5
s(2) = v0t(2) + at(2)²0,5
Где а ; v0 постоянные постоянные величины ( ускорение и начальная скорость тела ( соответственно ) ) ( подставим численные значения и решим систему )
40 = v0 5 + a 5² * 0,5
130 = v0 10 + a 10² * 0,5
Упростим
40 = 5v0 + 12,5а
130 = 10v0 + 50a
Разделим обе части уравнения на 5
8 = v0 + 2,5a | * ( -2 )
26 = 2v0 + 10a
-16 = -2v0 - 5a
26 = 2v0 + 10a
Суммируем две системы уравнения ( и получим одно уравнение )
10 = 5a
отсюда
а = 2 м/с²
Подставим численное значение ускорения в уравнение 8 = v0 + 2,5a и решим относительно начальной скорости тела
8 = v0 + 5
отсюда
v0 = 3 м/с
Первая задача: 2,0
Вторая задача: 124
Объяснение:
Первая задача
p(давление)=ро(плотность керосина)*g(ускорение свободного падения)*h(высота)
p(давление)=F(cила)/S(площадь)
F(cила)=m(масса керосина)*g(ускорения свободного падения)
Далее выводим формулу для высоты
(*) h=((mg)/S)/(ро*g)
Массу считаем 4,8 тонн=4800 кг
h=((4800*10)/3)/(800*10)=2м
Просят округлить до десятых, значит 2,0 м
Вторая задача
Выводим формулу для массы через высоту из формулы (*)
m=h*S*po
m=0,8*3*800=1920 кг
Переводим в тонны m=1,92 тонны
Далее будем опираться на прикрепленный рисунок
Так как по графику мы не можем определить время при 1,92 тонн, то воспользуемся треугольником АБC
tg(<Б)= 3,6/(3-1)=1,8
Так же
tg(<Б)=m/t1
Откуда t1=m/tg(Б)
t1=1,92/1,8=16/15 ч
Так как мы взяли треугольник с 1 ч, то полное время t=t1+1
=> t=(16/15)+1=31/15 ч
Нас просят дать ответ в минутах t=(31/15)*60= 124 минуты