Объём полости ≈ 940 мм³
Объяснение:
Медный шарик в воздухе весит 5,34 Н, а в пресной воде 4,34 Н. Определить объем полости внутри шарика?
P₁ = 5.34 H
P₂ = 4.34 H
ρ₁ = 8960 кг/м³ - плотность меди
ρ₂ = 1000 кг/м³ - плотность воды
------------------------
ΔV - ? объём полости внутри шарика
------------------------
В воде вес шарика меньше, чем в воздухе, на величину архимедовой силы Fa = ρ₂ · g · V
Р₂ = P₁ - ρ₂ · g · V
Откуда объём шарика
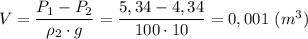
Вес шарика в воздухе
Р₁ = ρ₁ · g · (V - ΔV)
или
Р₁ = ρ₁ · g · V - ρ₁ · g · ΔV
Откуда объём полости

ПЕРВЫЙ
Спутник движется по круговой орбите, а значит имеет постоянное центростремительное ускорение, определяемое гравитацией. Обозначим радиус Земли, как R, высоту на Землёй, как H и r=R+H :
Сила притяжения:
F = GMm/r² = (GMm/R²) R²/r² = mgR²/r² ;
Центростремительное ускорение:
F/m = a = v²/r ;
gR²/r² = v²/r ;
r²/v² = r³/[gR²] ;
T² = (2πr/v)² = 4π²r³/[gR²] ;
T = 2πr/R √[r/g] = 2π/R √[(R+H)³/g] ;
T = 2π/R √[(R+H)³/g] ≈ [ π / 3 200 000 ] √[( 6 400 000 + 1 600 000 )³ / 9.8 ] ≈
≈ [ 5 000 π / 7 ] √10 ≈ 7100 сек ≈ 118 мин ≈ 1 час и 58 мин ;
ВТОРОЙ
Первая космическая скорость (околоземные спутники) равна VI = √[Rg] ;
Период околоземного спутника:
TI = 2πR/VI = 2πR/√[Rg] = 2π√[R/g] ;
По закону Кеплера для единого гравитационного центра верно, что:
T²/TI² = r³/R³ ;
T² = r³/R³ TI² = 4π² [r³/R³]*[R/g] = 4π²r³/[gR²] ;
T = 2πr/R √[r/g] = 2π/R √[(R+H)³/g] ;
T = 2π/R √[(R+H)³/g] ≈ [ π / 3 200 000 ] √[( 6 400 000 + 1 600 000 )³ / 9.8 ] ≈
≈ [ 5 000 π / 7 ] √10 ≈ 7100 сек ≈ 118 мин ≈ 1 час и 58 мин .