Question

Умоляю хотя бы что-нибудь решить по , 9 кл, все ! 1) автомобиль движется со скоростью 72 км/ч по закругленному участку дороги радиусом 100м. чему равен вес арбуза, находящегося в салоне, если его масса 10 кг? 2) пловец усиленно гребет руками стараясь плыть против течения. однако относительно берегов он остаётся на месте. импульс пловца равен а. относительно системы отсчёта, связанной с пловцом, плывущим по течению б. относительно системы отсчёта, связанной с берегом реки в. относительно системы отсчёта, связанной с пловцом, плывущим по течению и с берегом реки г. ни с одним из указанных систем отсчета 3) 2 тележки мас сами 2m и m движутся по гладкой горизонтальной поверхности о скоростями соответственно 4v и v. после того как первая тележка нагонит вторую, они обе соединяются. чему равна общая скорость тележек после соударения? 4) скатившись с горки высотой 1,5 м и длиной склона 25 м, вагон массой 20 т ударяет неподвижный вагон массой 25 т. трение пренебрежимо мало. с какой скоростью стал двигаться второй вагон после автосцепки?

Answer 1

1) Центростремительное ускорение = а = v^2/R

Скорость из км/ч переводим в м/с v=72*1000/3600=20м/с   тогда а=20^2/100=4м/с^2

Тогда вес арбуза=M*(g+a)=10кг*14м/с^2=140Н

2) Б     Т.к в условии сказано что относительно берегов он остаётся на месте, а значит относительно берега его скорость=0 а значит M*V -формула импульса = M*0=0

3) Закон сохранения импульсов 2m*4v+m*v=(2m+m)*x    

9mv=3m*x  выражаем х и получаем x=9mv/3m=3v

ответ. Скорость после соударения равна 3v

4) По закону сохранения энергии  mgh=mv^2/2    Отсюда выражаем скорость вагона который скатывался с горки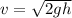  $v=}\sqrt{2gh}$

Далее по закону сохранения импульсов m-(вагон который скатывался) M-(который стоял на месте)   mv+M*0=(m+M)*x

x=mv/(m+M)=0.24м/с