а = 1 2/5 м - одна сторона треугольника
b = 5/7 м - вторая сторона треугольника
с = 1 2/35 м - третья сторона треугольника
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
а) Р = a + b + c = 1 2/5 + 5/7 + 1 2/35 = 1 14/35 + 25/35 + 1 2/35 = 2 41/35 = 3 целых 6/35 м - периметр треугольника;
b) Произведение взаимно обратных чисел равно единице (правило).
1 2/5 · 5/7 = 7/5 · 5/7 = 35/35 = 1
1 2/35 · 5/7 = 37/35 · 5/7 = (37·1)/(7·7) = 37/49
1 2/5 · 1 2/35 = 7/5 · 37/35 = (1·37)/(5·5) = 37/25 = 1 12/25
1 целая 2/5 и 5/7 - взаимно обратные числа, так как их произведение равно единице;
с) 1 2/5 = 1 14/35
1 2/5 > 1 2/35, так как 1 14/35 > 1 2/35
b < c < a, так как 5/7 < 1 2/35 < 1 2/5.
Пошаговое объяснение:
рассмотрим функцию f(x)=2x+(1/x²)-25,4
1) найдем производную
f'(x)=2-(2/x³)=(2x³-2)/x³=2(x³-1)/x³
правильный ответ первый
f'(x)=0 ; x³-1=0; x=1
при x>1 например x=2 ; f'(x)=2(8-1)/8=7/4>0 функция возрастает
при x∈(0;1) например 0.5 y'=2(0,125-1)/0,125<0 функция убывает
при х∈(-∞;0) например х=-1 ; f'(x)=2(-1-2)/-1>0 функция возрастает
2) f'(x)<0 при x∈(0;1)
3) на заданном интервале (0;1) функция убывает
при х=0,2 ; f(x)=2*0,2+(1/0,04)-25,4=0
так как при x∈(0;1) функция убывает а в точке х=0,2 функция равна 0 то это означает что при x∈(0;0,2) f(x)>0
2x+(1/x²)-25,4>0
2x+(1/x²)>25,4
что и требовалось доказать
4) для убывающей функции при х₁>x₂ f(x₁)<f(x₂)
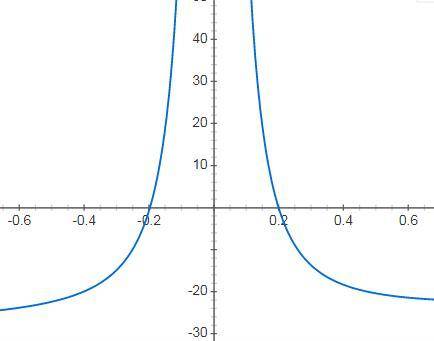
в качестве иллюстрации прилагается график функции
х^2+3х-88=0
D=9-352=361
x1=(-3-19)/2=-11
x2=(-3+19)/2=8
при пересечении с Оу х=0
у=-88