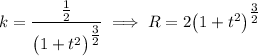Вкакой точке кривой y^2=16x ордината возрастает в 4 раза быстрее, чем абсцисса? абцисса это горизонтальная ось х, ордината это вертикальная ось y если принять что delta(y)/delta(x)= dy/dx = 4 то необходимо найти производную по переменной х выразим у из уравнения параболы у = 4x^(1/2)(возрастающая часть параболы расположена над осью ох) у = -4x^(1/2)(убывающая часть параболы расположена под осью ох) находим производную возрастающей части y' = (4x^(1/2))'= 4*(1/2)*x^(-1/2) =2/x^(1/2) 2/x(1/2) =4 находим х x^(1/2)=1/2 x=1/4 =0,25 найдем y y=4*(1/2)=2 в точке(1/4; 2) ордината возрастает в 4 раза быстрее, чем абсцисса
тело плавает, значит сила Архимеда равна силе тяготения, значит р(ро)жидкости*g*Vтела=mg, из этого выходит, что pжидкости*Vтела=mтела. Распишем масу как формулу.
после этого пошли гулять ошибки потому что Vт не равно Vж которую тело вытесняет
pжидкости*Vтела=ртела*Vтела,-грубая ошибка рж*Vж=pт*Vт рт=pж*Vж/Vт значит для нахождения плотности тела надо: 1) найти объем всего тела погрузив его полностью в жидкость ( с мензурки) Vт 2) поместить тело в мензурку и найти объем жидкости которую вытесняет тело при плавании Vж 3) зная плотность жидкости pж вычислить плотность тела
При движении по кривой ускорение материальной точки складывается из нормальной составляющей и тангенциальной (причем они ортогональны):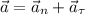
Найдём модули всех указанных векторов.
1)
2) , где
, где 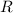 - радиус кривизны в данной точке (момент времени). Причём,
- радиус кривизны в данной точке (момент времени). Причём,  . Таким образом,
. Таким образом, 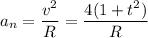
3)
Поскольку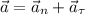 и
и  , то из прямоугольного треугольника на трёх указанных векторах получим:
, то из прямоугольного треугольника на трёх указанных векторах получим:
ответ.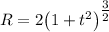
PS. Наиболее быстро ответ можно получить с дифференциальной геометрии.
Кривизной траектории выраженной явно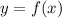 называется величина
называется величина 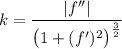 , а радиусом кривизны - величина
, а радиусом кривизны - величина 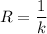 .
.
Для нашей задачи,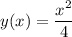 . Отсюда
. Отсюда 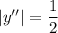 и
и 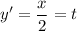 .
.
Сразу же получаем