Запишем уравнения движения тела по оси y:
y=v0sinα⋅t—gt22
Заменяя в уравнении y на данное h, получим квадратное уравнения, которое необходимо решить для нахождения времени полета. Неудивительно, что уравнение имеет 2 корня, поскольку на данной высоте тело за все время полета будет находиться 2 раза, что видно из рисунка.
h=v0sinα⋅t—gt22
gt2—2v0sinα⋅t+2h=0
Найдем дискриминант:
D=4v20sin2α—8gh
Проверять положительность дискриминанта не будем, поскольку решение задачи быть должно, значит он априори неотрицателен.
Тогда корни квадратного уравнения равны:
t=2v0sinα±4v20sin2α—8gh−−−−−−−−−−−−√2g
Мы получили ответ в общем виде. Теперь подставим все известные величины в СИ:
t=2⋅10⋅sin30∘±4⋅102⋅sin230∘—8⋅10⋅1,05−−−−−−−−−−−−−−−−−−−−−−−√2⋅10
Получаем два корня:
[t=0,7сt=0,3с
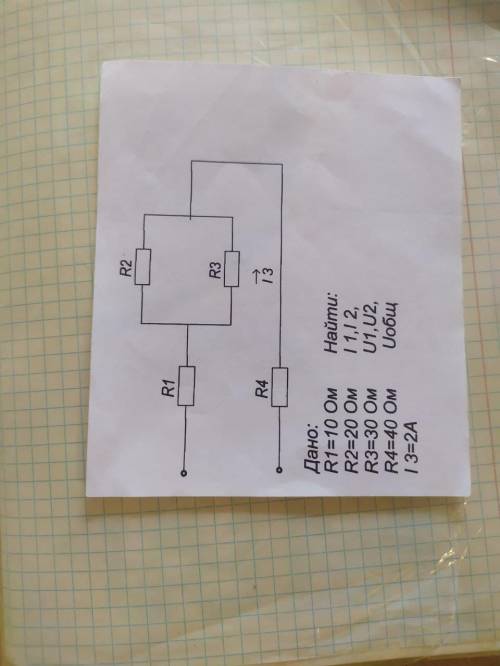
I1=A I2=3A U1=50B U2=60B U(общ)=310В
Объяснение:
Закон Ома:
U=IR
U3=I3R3
U3=30*2=60 В
Резеистеры R2 u R3 параллельны. Следовательно Напряжения равны U2=U3= 60 В =U(2-3)
U2=I2R2 Отсюда
I2=3A
I(2-3)=I2+I3
I(2-3)=3+2=5A
Резистеры R1, R(2-3),R3 соедениены последовательно, след. I1=I(2-3)=I4=5A
U1=I1R1
U1=5*10=50B
U2=I2R2
U4=I4R4
U4=5*40=200B
Uoбщ=U1+U(2-3)+U4
Uoбщ=50+200+60=310B