Когда растает льдинка в первом сосуде, уровень воды в первом сосуде опустится
Когда растает льдинка во втором сосуде, уровень воды во втором сосуде опустится
Объяснение:
Пусть плотность льда  , объем льда
, объем льда 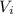 , плотность наполнителя полости (воздуха или свинца)
, плотность наполнителя полости (воздуха или свинца)  , объём полости
, объём полости 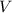 , плотность воды
, плотность воды 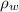 . Можно считать, что сосуд цилиндрический с площадью сечения S.
. Можно считать, что сосуд цилиндрический с площадью сечения S.
Сначала льдинка плавает так, чтобы сила Архимеда компенсировала силу тяжести. Найдём объём погружённой в воду части  :
:
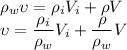
После таяния льда в сосуд добавится вода объёмом
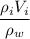 ,
,
а также во втором случае 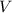 свинца
свинца
1) Наполнитель - воздух. Изменение уровня воды:
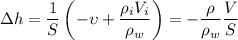
Плотность воздуха хоть и невелика, но всё же отлична от нуля, значит, высота уменьшится.
2) Наполнитель - свинец. Изменение уровня воды:

Выражение в скобках меньше нуля, значит, и в этом сосуде уровень воды тоже понизится
Когда растает льдинка в первом сосуде, уровень воды в первом сосуде опустится
Когда растает льдинка во втором сосуде, уровень воды во втором сосуде опустится
Объяснение:
Пусть плотность льда , объем льда , плотность наполнителя полости (воздуха или свинца) , объём полости , плотность воды . Можно считать, что сосуд цилиндрический с площадью сечения S.
Сначала льдинка плавает так, чтобы сила Архимеда компенсировала силу тяжести. Найдём объём погружённой в воду части :
После таяния льда в сосуд добавится вода объёмом
,
а также во втором случае свинца
1) Наполнитель - воздух. Изменение уровня воды:
Плотность воздуха хоть и невелика, но всё же отлична от нуля, значит, высота уменьшится.
2) Наполнитель - свинец. Изменение уровня воды:
Выражение в скобках меньше нуля, значит, и в этом сосуде уровень воды тоже понизится
Запишем силы, действующие на трос в воздухе, спроецировав их на ось Ох, направленную вверх, и запишем 2-ой закон Ньютона:
Поскольку плотность воздуха значительно меньше за плотность воды, то силой Архимеда, которая действует в воздухе, можно принебречь.
Запишем векторно второй закон Ньютона и на трос в воде:
Выразим T из двух уравнений:
Приравняем правые части:
За плотность стали возьмем число 8000 кг/м³ для удобства исчислений
[h₂/h₁] = (кг/м³)/(кг/м³) = 1
ответ: в 8/7 раза