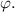 Поперечная к петле сила, действующая на кабинку, складывается из силы нормальной реакции и тяжести:
Поперечная к петле сила, действующая на кабинку, складывается из силы нормальной реакции и тяжести: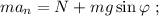
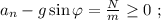
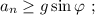
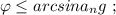
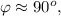 т.е. в самой верхней точке, то отрыв не произойдёт ни в одной точке.
т.е. в самой верхней точке, то отрыв не произойдёт ни в одной точке.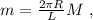 где
где 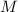 – масса всей сцепки.
– масса всей сцепки.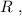 а значит, потенциальная энергия возрастёт по сравнению с горизонтальным участком на:
а значит, потенциальная энергия возрастёт по сравнению с горизонтальным участком на: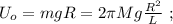
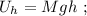
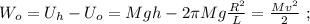
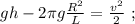
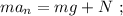
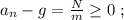
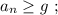
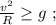
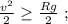
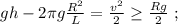
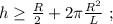
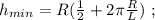
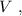
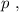
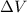 и
и 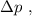
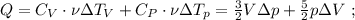
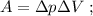
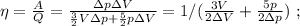
k=U1/U2=660 В. /380 В. =1,7
I1=S/U1=10000 В. *А. /660 В. =15 А.
I1=S/U2=10000 В. *А. /380 В. =26 А.
Объяснение: