Дано:
v1 = 1 м/с
v2 = 0,5 м/с
L = 1 м
Найти:
w = ? рад/с
v = w*R => w = v/R
w1 = v1/R1
w2 = v2/R2
Очевидно, что w1 = w2 = w, т.к. вращательное движение стержня равномерное (в условиях не говорится, что линейные скорости обоих концов меняют своё значение, значит они - постоянны) и угловая скорость всех точек в таком случае одинаковая. Запишем радиусы через длину стержня и выразим радиус одного из концов:
L = R1 + R2 => R1 = L - R2
Приравняем значение w1 к значению w2 и выразим радиус второго конца стержня:
w1 = w2
v1/(L - R2) = v2/R2
L - R2 = (v1*R2)/v2
L = (v1*R2)/v2 + R2 = (v1*R2 + v2*R2)/v2
L*v2 = v1*R2 + v2*R2 = R2*(v1 + v2)
R2 = L*v2/(v1 + v2).
И т.к. w = w2, то:
w2 = v2/R2 = v2 : L*v2/(v1 + v2) = (v1 + v2)/L = (1 + 0,5)/1 = 1,5 рад/с
ответ: угловая скорость стержня равна 1,5 рад/с.
Объяснение:
Пусть рабочим телом является 1 моль идеального газа, находящийся в следующих состояниях для четырех характерных точек А, В, С, D цикла Карно. Учтем, что на участках АВ и ВС газ расширяется (из рисунка видно, что давление падает), то есть совершает положительную работу, а на участках CD и DA работа отрицательна. На участке ВС: A(BC)=-dU=-cv(Tx - Tr), а на участке DA: A(DA)=-cv(Tr - Тх). Для обратимого процесса dU=0 и при нахождении общей работы за цикл A(BC) и A(CD) сокращаются, и остается только разность Q(AB)-Q(CD) при изотермических процессах (при Т(АВ) и T(CD)). Поэтому А= Q(AB)-Q(CD).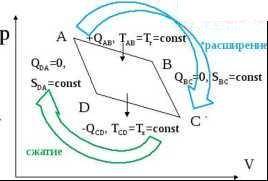
F=10 Н
Объяснение:
ma1=mg*sinα
ma2=F-mg sinα
a1= a2
Сложим эти уравнения
F= 2 ma=2*1*5=10 Н