Объяснение:
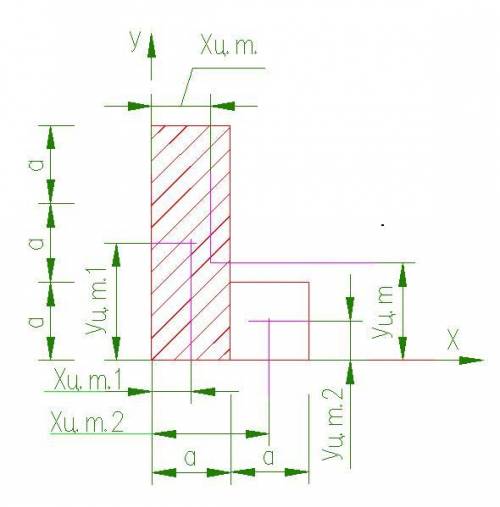
Пластина делится на две прямоугольные части.
У прямоугольника центр тяжести в середине.
У первой - заштрихованной пластины площадь 3a^2
А расстояния от координатных осей до центра тяжести:
Хцт1=0,5а
Уцт1=1,5а
У второй пластины площадь a^2
расстояния от координатных осей до центра тяжести:
Хцт2=1,5а
Уцт1=0,5а
Центр тяжести можно найти если просуммировать площади умноженные на расстояние до центра тяжести каждой простой фигуры, а потом эту сумму поделить на общую площадь.
Общая площадь фигуры 4а^2
Остается посчитать
Хц.т.=(3a^2*0,5а+a^2*1,5а)/4а^2=3а^3/4а^2=3а/4=0,75а
Уц.т.=(3a^2*1,5а+a^2*0,5а)/4а^2=3а^3/4а^2=5а/4=1,25а
Картинка приложена
Парціа́льний тиск (від лат. partialis — частковий) — внесок газу певного роду в загальний тиск суміші газів і відповідає тиску, під яким перебував би газ, що входить до складу газової суміші, коли б він один займав об'єм, рівний об'ємові суміші при тій самій температурі.
Парціальний тиск окремої складової частини (компонента) суміші, якщо її можна вважати ідеальним газом, визначається за формулою:
{\displaystyle p_{i}=\nu _{i}{\frac {RT}{V}},}{\displaystyle p_{i}=\nu _{i}{\frac {RT}{V}},}
де {\displaystyle \nu _{i}}{\displaystyle \nu _{i}} — кількість речовини даної (і-тої) компоненти, R — газова стала, T і V — відповідно, температура та об'єм суміші.
Згідно із законом Дальтона у випадку ідеальних газів парціальні тиски окремих компонентів суміші газів сумуються
{\displaystyle p=\sum _{i}p_{i}\,.}{\displaystyle p=\sum _{i}p_{i}\,.}
Парціальний тиск кожного із компонентів пропорційний частці цього компонента в суміші газів.
{\displaystyle p_{i}=x_{i}p}{\displaystyle p_{i}=x_{i}p},
де
{\displaystyle x_{i}={\frac {\nu _{i}}{\nu }}}{\displaystyle x_{i}={\frac {\nu _{i}}{\nu }}},
{\displaystyle \nu _{i}}{\displaystyle \nu _{i}} — кількість речовини i-го газу в суміші, {\displaystyle \nu }\nu — загальна кількість речовини газу.