Запишем уравнения движения тела по оси y:
y=v0sinα⋅t—gt22
Заменяя в уравнении y на данное h, получим квадратное уравнения, которое необходимо решить для нахождения времени полета. Неудивительно, что уравнение имеет 2 корня, поскольку на данной высоте тело за все время полета будет находиться 2 раза, что видно из рисунка.
h=v0sinα⋅t—gt22
gt2—2v0sinα⋅t+2h=0
Найдем дискриминант:
D=4v20sin2α—8gh
Проверять положительность дискриминанта не будем, поскольку решение задачи быть должно, значит он априори неотрицателен.
Тогда корни квадратного уравнения равны:
t=2v0sinα±4v20sin2α—8gh−−−−−−−−−−−−√2g
Мы получили ответ в общем виде. Теперь подставим все известные величины в СИ:
t=2⋅10⋅sin30∘±4⋅102⋅sin230∘—8⋅10⋅1,05−−−−−−−−−−−−−−−−−−−−−−−√2⋅10
Получаем два корня:
[t=0,7сt=0,3с
 м ;
м ;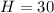 м .
м . ;
; .
.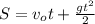 :
: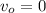 , а значит:
, а значит:  ;
; , откуда:
, откуда: 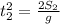 ;
;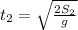 ;
;![t_2 = \sqrt{ \frac{ 2 * 2 [ {}_M ] }{ 9.8 [ {}_M/c^2 ] } } = 0.64 c](/tpl/images/0478/7687/31fb6.png) .
.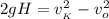 :
: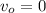 , а значит:
, а значит: 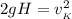 ;
;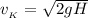 ;
;![v_{_K} = \sqrt{ 2 * 9.8 [ {}_M/c^2 ] * 30 [ {}_M ] } = 24](/tpl/images/0478/7687/9f655.png) м/с ;
м/с ;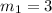 кг ;
кг ; ;
;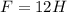 ;
;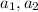 .
.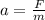 ;
;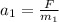 ;
; ;
;![a_1 = \frac{12H}{ 3 [ {}_{ K \Gamma } ] } = 4](/tpl/images/0478/7687/b6139.png) м/с² ;
м/с² ; м/с²
м/с²  м/с² ;
м/с² ; м/c ;
м/c ; .
.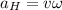 , где
, где 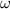 – угловая скорость часовой стрелки.
– угловая скорость часовой стрелки.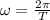 , где T – период вращения часовой стрелки.
, где T – период вращения часовой стрелки.
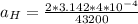 м/с²
м/с² 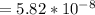 м/с²
м/с² 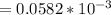 мм/с²
мм/с² 
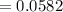 мкм/с²
мкм/с²  нм/с² ;
нм/с² ; м ;
м ;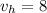 м/с .
м/с .
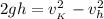 :
: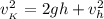 ;
;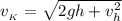 ;
;![v_{_K} = \sqrt{ 2gh + v_h^2 } = \sqrt{ 2 * 9.8 [ {}_M/c^2 ] * 2.9 [ {}_M ] + 8^2 [ {}_{M^2} / {}_{c^2} ] } =](/tpl/images/0478/7687/aa6ad.png)
![= \sqrt{ 121 [ {}_{M^2} / {}_{c^2} ] } = 11](/tpl/images/0478/7687/f565f.png) м/с ;
м/с ;
1. Вещества состоят из молекул - мельчайших частиц данного вещества.
2. Диффузия доказывает молекулярное строение веществ.
3. Объём тела увеличится при увеличении расстояния между частицами.
4. Фотографии электронного микроскопа доказывают малые размеры молекул.