Физика: Где располагается спираль в еликто чайнике?

Где располагается спираль в еликто чайнике?

👇

Увидеть ответ

Ответ:

кошка372

16.05.2023

Внутри внизу чайника у дна чайника

4,6(73 оценок)

Открыть все ответы

Ответ:

zifu

16.05.2023

1)Єнергия фотоєлектронов

E = m*v^2/2 = 9,11*10^(-31)*(2,5*10^6)^2/2 = 28,47*10^(-19) Дж

Работу выхода переведем в джоули

A = 2,39*1,6*10^(-19) = 3,824 *10^(-19) Дж

Энергия фотонов

E1 = E + А = (28,47 + 3,824)*10^(-19) = 32,294*10^(-19) Дж

Частота света

v = E/h = 32,294*10^(-19)/6,626*10^(-34) = 4,87*10^(15) Гц

2)Энергия фотона

E = h*v = 6,626*10^(-34)*10^(12) = 6,626*10^(-22) Дж

Масса фотона

m =h*v/c^2 = 6,626*10^(-34)*10^(12)/(3*10^8)^2 = 0,7362*10^(-38) Дж/с^2

Импульс фотона

p = h*v/c = 6,626*10^(-34)*10^(12)/(3*10^8) = 2,209*10^(-30) Дж/с

4,7(32 оценок)

Ответ:

akur12

16.05.2023

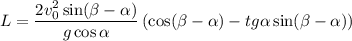
ответ: $L=\dfrac{2v_{0}^{2} \sin(\beta -\alpha )}{g \cos\alpha }\left(\cos(\beta -\alpha )- tg\alpha\sin(\beta -\alpha)} \right)$

Объяснение:

Несколько уточним условие: миномет находиться у подножия горы.

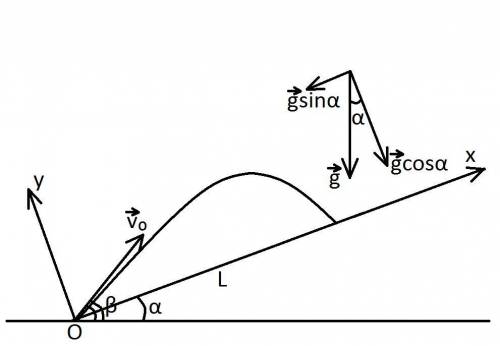
Выбираем систему координат как показано на рисунке. При перемещении тела(мины) выпущенного из миномета, оно будет участвовать как в движении вдоль оси Ox, так и вдоль оси Oy.

При этом, такое движение в данной системе отсчета, можно описать следующим образом.

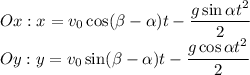
$Ox: x=v_{0} \cos(\beta -\alpha )t-\dfrac{g \sin\alpha t^{2} }{2} \\Oy: y=v_{0} \sin(\beta -\alpha )t-\dfrac{g \cos\alpha t^{2} }{2}$

Где t - время движения тела.

Рассмотрим более подробно движение вдоль оси Oy, определим в какие моменты времени $\tau$ координата, вдоль этой оси, будет равна 0.

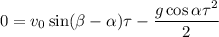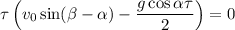
$0=v_{0} \sin(\beta -\alpha ) \tau -\dfrac{g \cos\alpha \tau^{2} }{2}$ ⇒ $\tau \left( v_{0} \sin(\beta -\alpha )-\dfrac{g \cos\alpha \tau}{2}\right)=0$

Отсюда получим 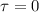$\tau=0$ (в начальный момент времени) или $\tau=\dfrac{2v_{0} \sin(\beta -\alpha )}{g \cos\alpha }$ (1)(в конечный момент времени)

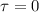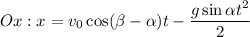$\tau=0$ нас мало интересует, поэтому в дальнейшем будем рассматривать только второй корень $\tau=\dfrac{2v_{0} \sin(\beta -\alpha )}{g \cos\alpha }$ , по этого времени координата тела вдоль оси Ox станет максимальной, то есть эта координата и будет расстоянием от миномета, до того места, на котором будут падать мины. 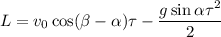Соответственно, так как $Ox:x=v_{0} \cos(\beta -\alpha )t-\dfrac{g \sin\alpha t^{2} }{2}$ , то $L=v_{0} \cos(\beta -\alpha )\tau-\dfrac{g \sin\alpha \tau^{2} }{2}$ . 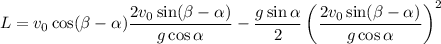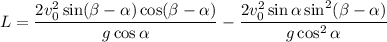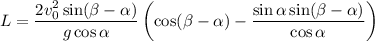Согласно уравнению (1) получим $L=v_{0} \cos(\beta -\alpha )\dfrac{2v_{0} \sin(\beta -\alpha )}{g \cos\alpha }-\dfrac{g \sin\alpha }{2}\left(\dfrac{2v_{0} \sin(\beta -\alpha )}{g \cos\alpha }\right)^{2}$ ⇒ $L= \dfrac{2v_{0}^{2} \sin(\beta -\alpha )\cos(\beta -\alpha )}{g \cos\alpha }-\dfrac{2v_{0}^{2} \sin\alpha \sin^{2} (\beta -\alpha)}{g \cos^{2}\alpha }}$ ⇒ $L=\dfrac{2v_{0}^{2} \sin(\beta -\alpha )}{g \cos\alpha }\left(\cos(\beta -\alpha )- \dfrac{\sin\alpha \sin(\beta -\alpha)}{\cos\alpha} \right)$ ⇒ $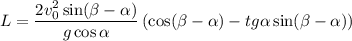L=\dfrac{2v_{0}^{2} \sin(\beta -\alpha )}{g \cos\alpha }\left(\cos(\beta -\alpha )- tg\alpha\sin(\beta -\alpha)} \right)$