Из условия видно, что период увеличивается, следовательно лифт должен двигаться с ускорением, направленным вертикально вниз. (Данный факт следует из формул о весе тела, его движении вверх, или вниз с ускорением, так же, можно получить из второго закона Ньютона, расписывая силы, действущие на груз, который подвешен на математическом маятнике). ( длина маятника (l) - величина постоянная).
Запишем формулу периода математического маятника:
Теперь запишем данную формулу для двух случаев:
Возведем в квадрат и правую и левую часть каждого уравнения:
На заряженную частицу в электростатическом поле действует кулоновская сила, которую можно найти, зная напряженность поля в данной точке: . эта сила сообщает ускорениегде m — масса заряженной частицы. как видно, направление ускорения будет совпадать с направлением , если заряд частицы положителен (q > 0), и будет противоположно , если заряд отрицателен (q< 0). если электростатическое поле однородное ( = const), то ускорение a= const и частица будет совершать равноускоренное движение (при отсутствии других сил). вид траектории частицы зависит от начальных условий. если вначале заряженная частица покоилась или ее начальная скорость сонаправлена с ускорением , то частица будет совершать равноускоренное прямолинейное движение вдоль поля и ее скорость будет расти. если , то частица будет тормозиться в этом поле. если угол между начальной скоростью и ускорением острый 0 < α < 90° (или тупой), то заряженная частица будет двигаться по параболе. во всех случаях при движении заряженной частицы будет изменяться модуль скорости, а следовательно, и кинетическая энергия частицы. 1. заряженная частица влетает в магнитное поле со скоростью , направленной вдоль поля или противоположно направлению магнитной индукции поля . в этих случаях сила лоренца и частица будет продолжать двигаться равномерно прямолинейно. 2. заряженная частица движется перпендикулярно линиям магнитной индукции тогда сила лоренца , следовательно, и сообщаемое ускорение будут постоянны по модулю и перпендикулярны к скорости частицы. в результате частица будет двигаться по окружности , радиус которой можно найти на основании второго закона ньютона:отношение — называют удельным зарядом частицы.период вращения частицыто есть период вращения не зависит от скорости частицы и радиуса траектории. 3. скорость заряженной частицы направлена под углом к вектору.движение частицы можно представить в виде суперпозиции равномерного прямолинейного движения вдоль поля со скоростью и движения по окружности с постоянной по модулю скоростью в плоскости, перпендикулярной полю. радиус окружности определяется аналогично предыдущему случаю, только надо заменить на , то естьв результате сложения этих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю. шаг винтовой линиинаправление, в котором закручивается спираль, зависит от знака заряда частицы. если скорость заряженной частицы составляет угол α с направлением вектора неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, тο r и h уменьшаются с ростом b. на этом основана фокусировка заряженных частиц в магнитном поле. если на движущуюся заряженную частицу помимо магнитного поля с индукцией действует одновременно и электростатическое поле с напряженностью , то равнодействующая сила, приложенная к частице, равна векторной сумме электрической силы и силы лоренца: . характер движения и вид траектории зависят в данном случае от соотношения этих сил и от направления электростатического и магнитного полей.
Дано:
T1= 1 секунда.
T2=1,1 cекунда.
a=?
_______
Из условия видно, что период увеличивается, следовательно лифт должен двигаться с ускорением, направленным вертикально вниз. (Данный факт следует из формул о весе тела, его движении вверх, или вниз с ускорением, так же, можно получить из второго закона Ньютона, расписывая силы, действущие на груз, который подвешен на математическом маятнике). ( длина маятника (l) - величина постоянная).
Запишем формулу периода математического маятника:
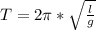
Теперь запишем данную формулу для двух случаев:
Возведем в квадрат и правую и левую часть каждого уравнения:
Поделим первое уравнение на второе:
Теперь выведем ускорение (а):
Посчитаем сначала периоды:
a=(g*(T2^2-T1^2)/(T1^2)=(g*(1,21-1)/(1,21)=0,17*g;
Подставляем значение ускорения свободного падения, равное, если быть более точным, 9,8 м/с^2.
a=0,17*9,8=1,666 м/с^2. Такое ускорение у лифтра. (если брать g=10м/с^2, то получим а=1,7 м/c^2).
ответ: а=1,666 м/с^2; (a=1,7 м/с^2).Лифт движется с ускорением, направленным вертикально вниз.