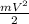Тело падает с некоторой высоты 6 секунд. какова эта высота?

👇

Ответ:

Миша112236677777777

05.08.2022

h=gt^2/2 h2-h1=v0t+gt^2/2 10=v0*1+10*1^2/2 10=vo+5 v0=5 начальная скорость на последней секунде полета или конечная до последней секунды из формулы конечной скорости при свободном падении имеем v=gt1^2/2 5=10*t1^2/2 5=5*t1^2 t1=1 время до последней секунды значит тело летело всего 2 секунды найдем высоту H=gt2^2/2=10*2^2/2=20 м

4,7(21 оценок)

Открыть все ответы

Ответ:

aruzhanormanova

05.08.2022

Скорость лопасти ограничивается 0,9 от скорости звука. С учётом того, что скорость лопасти от вращения складывается со скоростью перемещения вертолёта. То при скорости вертолёта 100м/сек она не может быть более 200м/сек. Есть ещё один ограничивающий фактор. воздушная скорость лопасти идущей назад не может быть слишком маленькой. Максимум отношение скорости =3.. Так на Ми-8 при радиусе лопасти 6 м о частоте вращения. 200об/мин скорость лопасти на взлёте около 120 м/сек. Что позволяет ему развить скорость около 60м/сек.

4,5(45 оценок)

Ответ:

Vexicy

05.08.2022

Полная энергия тела есть сумма потенциальной и кинетической энергий: Wпол = Wпот + Wкин. В момент падения Wпот = 0 (т.е. высота в момент падения = 0), значит осталось найти Wкин = $\frac{ mV^{2}}2$ , где масса известна. Найдем скорость тела в момент падения. 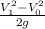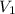Связь между изменением координаты и скоростью при равноускоренном движении (ускорение постоянно и равно ускорению свободного падения) выражается формулой Δy= $\frac{ V_{1} ^{2} - V_{0}^{2}}{2g}$ , где $V_{1}$ - скорость тела в момент падения, 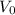$V_{0}$ - скорость с которой тело бросили. Поскольку мы не знаем, в каком направлении бросили тело (под каким углом к горизонту 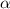$\alpha$ ), то в общем виде вышеуказанное выражение можно переписать как 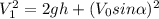$V_{1}^{2} =2gh+(V_{0}sin \alpha)^{2}$ , где Δy заменили на высоту h. Тогда окончательная формула для решения задачи будет: Wпол = Wкин = 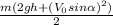$\frac{ m(2gh+(V_{0}sin \alpha)^{2})}2$ . Если тело бросили вертикально вверх или вертикально вниз, то Wпол = Wкин = 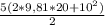$\frac{ 5(2*9,81*20+10^{2})}2$ =1231 Дж, если строго по горизонтали, то Wпол = Wкин = 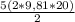$\frac{ 5(2*9,81*20)}2$ =981 Дж. В остальных случаях ответа на вопрос задачи требуется знать угол к горизонту, под которым тело бросили, и ответ будет в диапазоне от 981 до 1231 Дж.