Дано:
Время импульса t=10 мкс=10*10⁻⁶с=10⁻⁵с
Частота (ню)=60 МГц (мЕга)=60*10⁶=6*10⁷ Гц (1/с)
n - число волн - ?
Если известна частота, можно найти ее период
Т=1/(ню)
Тогда n=t/T=t*(ню) время всего импульса делим на период, время одного колебания, или умножаем на частоту
n=10⁻⁵ * 6*10⁷=6*10⁷⁻⁵=6*10²=600 - это ответ.
А) ответ:3 ,поясняю резисторы соединены параллельно,а значит общее сопротивление 1/R=1/2+1/2+1/2 выводя R получаем как раз 2/3
Б) ответ:4 Первые два резистора соединены параллельно их общее сопротивление равно 1/R=1/2+1/2 , где R=1 и прибавляем к еще одному резистору который соединен последовательно R=1+2=3
В) ответ:5. Сложим верхние два резистора так как они последовательно соединены получаем 4 и при параллельном 1/R=1/4+1/2 получаем R=4/3
Г)ответ:2 Тут просто просто складываем R=2+2+2=6
Если не понятно обращайся
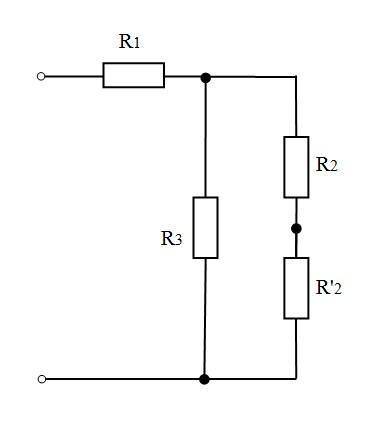
Схема состоит из:
группы сопротивлений R₂ и R₂', соединенных последовательно,
сопротивления R₃, соединенного параллельно с первой группой,
сопротивления R₁, соединенного последовательно с первыми двумя группами.
Преобразовать схему можно так: (см. рис.1)
Тогда общее сопротивление R₂ и R₂':
R₂₂ = R₂ + R₂' = 20 + 20 = 40 (Ом)
То есть сопротивления R₂ и R₂' можно заменить одним сопротивлением R₂₂ = 40 (Ом) (см. рис.2)
Общее сопротивление R₂₂ и R₃:
R₂₂₃ = R₂₂•R₃ : (R₂₂+R₃) = 40•60 : 100 = 24 (Ом)
Общее сопротивление цепи с учетом R₁:
R = R₁ + R₂₂₃ = 6 + 24 = 30 (Ом)
Общий ток в цепи:
I = I₁ = U/R = 240 : 30 = 8 (A)
Напряжение на первом сопротивлении:
U₁ = I · R₁ = 8 · 6 = 48 (B)
Напряжение на группе сопротивлений R₂₂₃:
U₂₂₃ = U - U₁ = 240 - 48 = 192 (B)
Ток, протекающий через R₃:
I₃ = U₂₂₃ : R₃ = 192 : 60 = 3,2 (A)
Ток, протекающий через R₂₂:
I₂₂ = U₂₂₃ : R₂₂ = 192 : 40 = 4,8 (A)
Напряжение на R₂ и R₂':
U₂ = U₂' = R₂I₂₂ = R₂'I₂₂ = 20 · 4,8 = 96 (B)
Дано:
t = 10 мкс = 10·10⁻⁶ с = 10⁻⁵ с
ν = 60 МГц = 60·10⁶ Гц = 6·10⁷ Гц
Найти N.
Решение.
ν = N/t
N = ν·t = 6·10⁷Гц·10⁻⁵с = 600.
Гц = с⁻¹