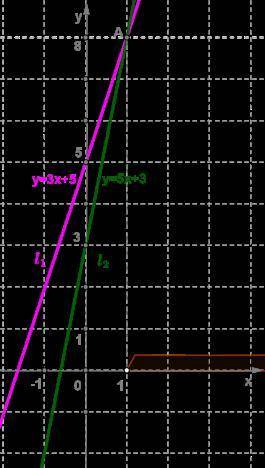
Для решения неравенства 3x+5<5x+3 построим графики линейных функций, расположенных в правой и левой части данного уравнения, т. е. построим графики y=3x+5 и y=5x+3.
Для построения графика каждой линейной функции составим таблицу значений.
Для функции y=3x+5 имеем:
x 0 1
y 5 8
Через полученные точки проведём прямую l1.
Для функции y=5x+3 имеем:
x 0 −1
y 3 −2
Через полученные точки проведём прямую l2.
Прямые y=3x+5 и y=5x+3 пересекаются в точке A(1;8). В этой точке значения функций равны.
Используя построение, делаем вывод: для того чтобы значение первой функции было меньше значения второй функции, необходимо, чтобы первый график был ниже второго, т. е. при x>1.
Можно проверить ответ, полученный при построении, решая неравенство:
3x+5<5x+3;3x−5x<3−5;−2x<−2;x>1.
Объяснение:
Объяснение:
Дано:
U = 120 B
q = 2 мкКл = 2·10⁻⁶ Кл
d = 6 мм = 6·10⁻³ м
C - ?
E - ?
Электроемкость:
С = q / U = 2·10⁻⁶ / 120 ≈ 17·10⁻⁹ Ф или 17 нФ
Напряженность:
E = U / d = 120 / (6·10⁻³) = 20 000 В/м или 20 кВ/м