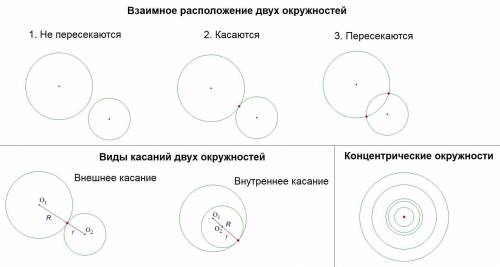
Пусть R, r -- радиусы двух окружностей, O₁, O₂ -- их центры.
1. Взаимное расположение двух окружностей
Выделяют три основных случая взаимного расположения окружностей:
Две окружности не имеют общих точек (не пересекаются)Две окружности имеют одну общую точку (касаются)Две окружности имеют две общие точки (пересекаются)Также выделяют иногда четвёртый случай: совпадающие окружности (бесконечное множество общих точек).
2. В каком случае окружности имеют одну общую точку?
Окружности будут иметь одну общую точку, если:
Сумма их радиусов равна расстоянию между центрами (R + r = O₁O₂).Разность их радиусов равна расстоянию между центрами (R - r = O₁O₂).3. Как называется общая точка двух окружностей?
Если окружности касаются в некоторой точке, то такая точка называется точкой касания.
Если пересекаются -- точкой пересечения.
4. Виды касаний двух окружностей
В пункте 2 было выделено два признака касания окружностей, откуда получается 2 вида касания:
Внешнее касание (R + r = O₁O₂)Внутреннее касание (R - r = O₁O₂)5. Когда окружности пересекаются?
Окружности пересекаются, когда расстояние между центрами меньше суммы радиусов, но больше их разности: R - r < O₁O₂ < R + r
6. Концентрические окружности
Окружности, имеющие общий центр, называются концентрическими.
Пусть R, r -- радиусы двух окружностей, O₁, O₂ -- их центры.
1. Взаимное расположение двух окружностей
Выделяют три основных случая взаимного расположения окружностей:
Две окружности не имеют общих точек (не пересекаются)Две окружности имеют одну общую точку (касаются)Две окружности имеют две общие точки (пересекаются)Также выделяют иногда четвёртый случай: совпадающие окружности (бесконечное множество общих точек).
2. В каком случае окружности имеют одну общую точку?
Окружности будут иметь одну общую точку, если:
Сумма их радиусов равна расстоянию между центрами (R + r = O₁O₂).Разность их радиусов равна расстоянию между центрами (R - r = O₁O₂).3. Как называется общая точка двух окружностей?
Если окружности касаются в некоторой точке, то такая точка называется точкой касания.
Если пересекаются -- точкой пересечения.
4. Виды касаний двух окружностей
В пункте 2 было выделено два признака касания окружностей, откуда получается 2 вида касания:
Внешнее касание (R + r = O₁O₂)Внутреннее касание (R - r = O₁O₂)5. Когда окружности пересекаются?
Окружности пересекаются, когда расстояние между центрами меньше суммы радиусов, но больше их разности: R - r < O₁O₂ < R + r
6. Концентрические окружности
Окружности, имеющие общий центр, называются концентрическими.

Решение. Так как треугольник АВС равнобедренный по условию и ∠ABC = 120°, то ∠BAC = ∠BCA = (180°-120°)/2 = 30°. Так как CM - биссектриса треугольника АВС, то ∠MCA = ∠ BCM = 15°.
Рассмотрим треугольник AMC. Из теоремы синусов: MC/sin30° = AM/sin15°. Выразим из пропорции длину стороны MC: MC = AM*sin30°/sin15° = 14*0,5/sin15° = 7/sin15° (см).
Пусть MH - перпендикуляр, проведенный из точки М к прямой ВС. Отрезок MH - искомое расстояние.
Рассмотрим треугольник МНС. ∠МНС = 90°, ∠НСМ = 15°. Выразим из этого треугольника длину катета МН: МН = MC*sin15° = 7*sin15°/sin15° = 7 (см).
ответ: 7 см.