1) R ≤ 1,176π м
2) ≈0,82 м от свинцового конца вала
Объяснение:
1) Учитывая ограниченность заданных условий, силой сопротивления воздуха и другими мелочами мы пренебрегаем.
Упрощенно имеем модель, где действуют 2 разнонаправленные силы.
Центробежная сила, перпендикулярная оси вращения и направленная от оси: Fцб.=m·ω·R, где m-масса предмета, ω-угловая скорость, R-радиус вращения.
Вызванная силой тяжести, сила трения (покоя?) направленная противоположно центробежной:
Fтр.=μ·m·g, где μ-коэффициент трения, m-масса предмета, g-ускорение свободного падения.
Для выполнения условия задачи, центробежная сила не должна превысить силу трения, поэтому получаем неравенство:
Fцб.≤Fтр. ⇒
m·ω·R ≤ μ·m·g ⇒
R ≤ μ·g÷ω
Осталось лишь преобразовать частоту вращения в угловую скорость.
ω=2·π·20/60 (2π-полный оборот в радианах, делим на 60 чтобы перевести минуты в секунды)
В итоге получаем:
R ≤ 0,08·9,8÷(2·π·20÷60)
R ≤ 1,176π м
или (R ≤≈3,694 м)
2) Имеем вал, длиной 2 метра, 1 метр-свинцовый, 1 метр -оловянный.
Масса свинцовой части m₁=11340*1*πR² (плотность свинца, умноженная на объём)
Масса оловянной части m₂=7260*1*πR².
Т.к. олово гораздо легче свинца, то центр тяжести будет сдвинут от геометрического центра вала на "свинцовую" половину.
Найдем разницу масс свинцовой и оловянной частей:
m₃=m₁-m₂=πR²(11340-7260)=4080·πR².
Значит центр масс будет сдвинут на половину длины свинцового участка вала с такой массой.
Найдем длину свинцового участка с массой 4080·πR²:
4080·πR² ÷ (11340·πR²)≈0,36 м
Значит центр тяжести расположен на 0,36/2=0,18 м ближе от середины к свинцовому концу вала, или (1-0,18)=0,82 м от свинцового конца вала
Дано:
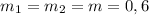 кг
кг
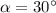
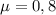
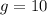 м/с²
м/с²
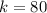 Н/м
Н/м
============================
Найти: 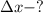
============================
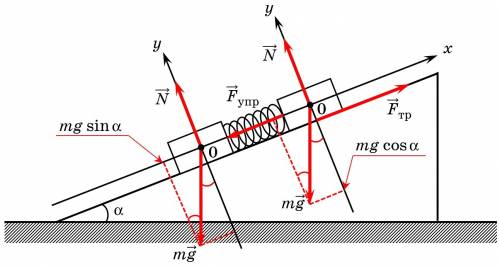
Решение. Рассмотрим один из двух маленьких брусков, так как они одинаковые. На брусок действуют три силы: сила тяжести 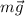 , сила трения
, сила трения 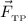 и сила упругости
и сила упругости 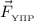 (см. рисунок).
(см. рисунок).
Свяжем систему координат с бруском на поверхности Земли, ось 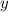 направим перпендикулярно поверхности плоскости, ось
направим перпендикулярно поверхности плоскости, ось  — вдоль поверхности (при таком выборе осей только одна сила
— вдоль поверхности (при таком выборе осей только одна сила 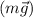 не лежит на осях координат).
не лежит на осях координат).
Если два бруска покоятся, то сложим геометрически эти три силы и приравняем их к нулю:
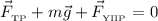
Спроецируем уравнение на оси координат (сила 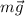 не лежит на оси координат, поэтому для нахождения её проекций опустим из конца вектора
не лежит на оси координат, поэтому для нахождения её проекций опустим из конца вектора 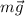 перпендикуляры на оси
перпендикуляры на оси  и
и 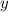 :
: 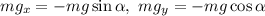 ) и запишем выражения для силы трения
) и запишем выражения для силы трения 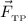 :
:
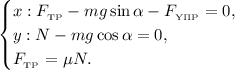
Распишем все силы, действующие на брусок:
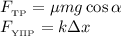
Подставим их в уравнение:
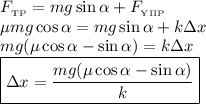
Определим значение искомой величины:
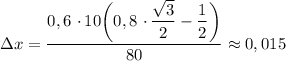 м
м
============================
ответ: 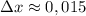 м
м
2.5 г/см в кубе=2500 кг/м в кубе
m=V*p
m= 10*2500=25000кг