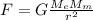 , где
, где 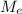 — масса Земли,
— масса Земли, 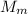 — масса Луны,
— масса Луны,  — радиус орбиты Луны.
— радиус орбиты Луны.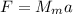 , где
, где  — центростремительное ускорение;
— центростремительное ускорение;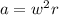 , где
, где 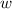 — угловая скорость;
— угловая скорость;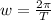 , где
, где 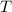 — период обращения Луны вокруг Земли.
— период обращения Луны вокруг Земли.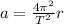
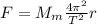
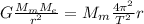
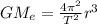
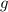 , и на основе вышеизложенного можем написать аналогичное уравнение
, и на основе вышеизложенного можем написать аналогичное уравнение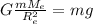 , где
, где 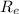 — радиус Земли;
— радиус Земли;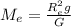
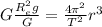
![r = \sqrt[3]{\frac{R_{e}^{2}T^{2}g}{4\pi^{2} }}](/tpl/images/4768/6654/2c10d.png)
Если мы пренебрегаем трением, то вдоль поверхности наклонной плоскости (параллельно ей) на тело действует только проекция силы тяжести. Значение данной проекции: F=m*g*sinα. Согласно второго закона Ньютона, эта сила определяет ускорение тела вдоль поверхности наклонной плоскости: a=F/m. Подставим F, получим: a=m*g*sinα/m=g*sinα.Длина пути : S=h/sinα (из прямоугольного треугольника). Также, если считать, что тело начинает соскальзывать из состояния покоя, то можно длину пути выразить как: S=a*t²/2. Выразим отсюда время соскальзывания: t=√((2*S)/a). Подставляем выражение для ускорения, полученное из второго закона Ньютона: t=√((2*S)/(g*sinα))=
Подставив выражение для S, получим: t=√((2*h)/(g*sin²α))=√((2*10)/(10*0,5*0,5))=√(20/2,5)=√8=2√2 сек=2,82 сек.
По закону всемирного тяготения сила взаимодействия
1)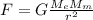 , где
, где 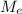 — масса Земли,
— масса Земли, 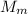 — масса Луны,
— масса Луны,  — радиус орбиты Луны.
— радиус орбиты Луны.
С другой стороны, Луна движется только с центростремительным ускорением, значит по II закону Ньютона
2)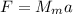 , где
, где  — центростремительное ускорение;
— центростремительное ускорение;
3)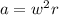 , где
, где 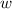 — угловая скорость;
— угловая скорость;
4)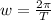 , где
, где 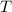 — период обращения Луны вокруг Земли;
— период обращения Луны вокруг Земли;
5)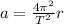
6)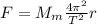
Тогда
7)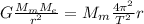
8)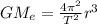
К слову, масса Земли, которая фигурирует в последней формуле, была вычислена в 1798 году Генри Кавендишем на основе уже известного в то время радиуса Земли. Радиус же Земли был вычислен опытным путём в 240 году до нашей эры Эратосфеном Киренским. Поэтому предлагаю перейти в нашей формуле от массы Земли к радиусу Земли. Мы знаем, что тело на поверхности Земли движется с ускорением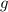 , и на основе вышеизложенного можем написать аналогичное уравнение
, и на основе вышеизложенного можем написать аналогичное уравнение
9)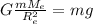 , где
, где 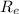 — радиус Земли;
— радиус Земли;
10)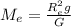
Подставим массу Земли в формулу 8.