Ведь всё очень просто, гляди
1. Общее уравнение пути от времени при равноускоренном движении такое
S(t) = S0 + v0*t + a*t*t/2. (Если возникает вопрос почему? это хорошо, ответ - 2 раза проинтегрируй a*dt, потому что ускорение (а) - вторая производная пути по времени, не умеешь интегрировать - поверь на слово).
Далее
1.1. Положим S0=0. Просто будем расстояние считать от 0, на так удобнее, хотя не во всех задачках это так.
1.2. V0=0, это дано в условии, так как тело начало двигаться из состояния ПОКОЯ, то есть без начальной скорости.
1.3. Подставив это в ОБЩУЮ формулу движения, получим формулу движения тела, определённого условиями задачи.
S(t) = a*t*t/2
Всё! Задача решена, потому что мы нашли общее уравнение движения нашего тела, дальше уже не физика, а примитивная арифметика для 1 класса.
2.1 По условию задачи известно, что
S(1)=S
а требуется найти S(2).
S(1)=a*1*1/2=a/2=S, откуда a = S*2.
S(2)= a*2*2/2=a*2=S*2*2=4*S.
Ну и всё.
ответ: за 2с тело пройдёт путь 4*S.
Задача №7
1. Введем прямоуголную систему координат следующим образом, полож. нарпавление оси Оу совпадает с направлением начальной скорости тела, а полож. направление оси Ох совпадает с направлением скорости тела через 5 с, то есть перпендикулярно (по усл.)
2. В векторном виде: S(суммарное)=S(по оси Ох)+S(по оси Оу).
Т.к. угол между векторами 90, то S(суммарное) найдем по теореме Пифагора, зная перемещение вдоль оси Ох, и перемещение вдоль оси Оу.
3. Пусть v0 - начальная скорость, v - скорость тела через время t=5с, y - перемещение тела вдоль оси Оу, х - перемещение тела вдоль оси Ох, угол а - угол между вектором v0 и горизонтом, (а также угол между вектором g и осью Ох), тогда:
Oy: 0=v0-g*sin a*t, где t = 5 c, то есть v0=g*sin a*t
Ox: v=0+g* cos a*t, то есть v=g*cos a*t
y=v0*t -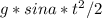 ; так как v0=g*sin a*t, то:
; так как v0=g*sin a*t, то:
y =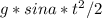
x=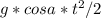
4. s=√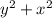
s=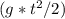 √
√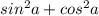 , согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:
, согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:
s=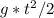
s=10*4*4/2=80(м)
ответ: 80 м