Объяснение:
--------------------------
1) в классической механике
Сразу же оговоримся о том что классическая механика не подразумевает работу с релятивистскими скоростями, а лишь со скоростями многим меньше скорости распространения света в вакууме. - но если в задании просят, то рассчитаем
В классической механике чтобы определить скорость сближения, в нашем случае, мы бы должны были просто сложить эти скорости
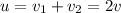
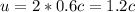
Таким образом у нас получилось скорость порядка 
м/с
Как видно мы получили скорость сближения ракет больше чем скорость распространения света в вакууме, а значит работать с релятивистскими скоростями в классической механике дело в корне неверное
2) в специальной теории относительности
А как раз в СТО работать с релятивистскими скоростями можно и нужно
Тут скорость сближения ракет будет вычисляется следующим образом
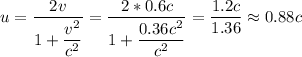
Таким образом у нас получилось скорость порядка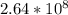 
м/с, что уже не противоречит постулатам СТО
Последовательное:
R(1,2)=R1+R2=15+5=20 Ом;
Параллельное:
R(1-2)=R5=20 Ом =>
R(1,2,5)=R(1,2)/2=R5/2=20/2=10 Ом;
R(1,2,5)=R4=10 Ом =>
R(1,2,4,5)=R(1,2,5)/2=R4/2=10/2=5 Ом;
R(1,2,4,5)=R3=5 Ом =>
R(1-5)=R(1,2,4,5)/2=R3/2= 5/2=2,5 Ом.
Последовательное:
Rобщ=R(1-6)=R6+R(1-5)=2,5+7,5=10 Ом.
I=I6=U/Rобщ=220/10=22 A;
U6=I*R6=22*7,5=165 B;
U3=U4=U5=U-U6=220-165=55 B;
I3=U3/R3=55/5=11 A;
I4=U4/R4=55/10=5,5 A;
I5=U5/R5=55/20=2,75 A;
I1=I2=I-I3-I4-I5=22-11-5,5-2,75=2,75 A.
P=U*I=220*22=4840 Вт≈4,8 кВт.
ΣP=I₁²*R₁+I₂²*R₂+I₃²*R₃+I₄²*R₄+I₅²*R₅+I₆²*R₆=
=2,75²*(15+5)+11²*5+5,5²*10+2,75²*20+22²*7,5=
=151,25+605+302,5+151,25+3 630=4 840 Вт≈4,8 кВт.
---
Т.к. P=4,8 кВт = ΣP=4,8 кВт,
то считаем, что баланс мощностей
имеет место быть, а расчёт
выполнен ПРАВИЛЬНО за
---
Фсё.