ответ: Никак не измениться
Объяснение:
Пусть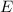 
- напряжённость электростатического поля создаваемым точечным зарядом 
. В некоторую точку этого электростатического поля помещают пробный заряд 
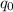
По определению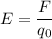 
Где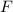 
- сила электростатического взаимодействия между двумя точечными зарядами и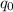
Согласно закону Кулона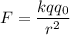 
Где 
- расстояние между точечными зарядами и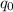
Преобразуем первую формулу
Как видно из итоговой формулы напряженность электростатического поля создаваемым точечным зарядом никак не зависит от значения модуля пробного заряда внесенного в это поле.
В принципе формулу можно было записать и самого начала и объяснить что так и так. Или даже вовсе не записывать и все объяснить словами.
Если имеется материальная точка Of, к которой приложена сила F, то момент силы относительно точки O равен векторному произведению радиус-вектора r, соединяющего точки O и Of, на вектор силы F.
Момент силы относительно оси:
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:
* длина вектора c равна произведению длин векторов a и b на синус угла между ними.
* вектор c ортогонален каждому из векторов a и b.
* вектор c направлен так, что тройка векторов {abc} является правой.
Таким образом, момент силы есть величина векторная. И вектор момента силы направлен так, чтобы из его конца вращение от а к b происходило против часовой стрелки.
Ну, думаю, я тебя здорово запутал. На практике эти все формулировки означают следующее.
Чтобы найти момент силы относительно точки, нужно:
- продлить мысленно линию действия силы вперед, или назад (по обстоятельствам),
- из точки вращения опустить перпендикуляр на линию действия силы, и найти его длину (вот тут как раз может пригодиться синус угла).
- умножить силу на длину перпендикуляра в одной системе единиц. Получишь величину момента силы.
Но не забывай, что это вектор. Он всегда перпендикулярен плоскости вращения, то есть плоскости, проходящей через точку вращения и линию действия силы. И направлен в ту сторону от плоскости, чтобы вращение под действием силы вокруг точки было видно с его конца против часовой стрелки.