Объяснение:
--------------------------
1) в классической механике
Сразу же оговоримся о том что классическая механика не подразумевает работу с релятивистскими скоростями, а лишь со скоростями многим меньше скорости распространения света в вакууме. - но если в задании просят, то рассчитаем
В классической механике чтобы определить скорость сближения, в нашем случае, мы бы должны были просто сложить эти скорости
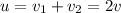
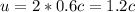
Таким образом у нас получилось скорость порядка 
м/с
Как видно мы получили скорость сближения ракет больше чем скорость распространения света в вакууме, а значит работать с релятивистскими скоростями в классической механике дело в корне неверное
2) в специальной теории относительности
А как раз в СТО работать с релятивистскими скоростями можно и нужно
Тут скорость сближения ракет будет вычисляется следующим образом
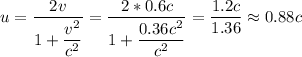
Таким образом у нас получилось скорость порядка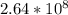 
м/с, что уже не противоречит постулатам СТО
Нас просят найти просто скорость (не пишут "найдите угловую скорость"). Значит это обычная линейная скорость. В движении по окружности формула линейной скорости имеет тот же смысл, что и формула скорости в равномерном прямолинейном движении:
V = S / t;
Только в нашем случае, S - это длина дуги окружности, а t - это период (время, за которое стрелка проходит один круг):
V = 2π*R / T
Время известно: секундная стрелка проходит один круг за 60 секунд, радиус равен длине стрелки - 20 см = 0,2 м, π = 3,14, решаем:
V = 2*3,14*0,2 / 60 = 0,020933 = 0,02 м/с
ответ: примерно 0,02 м/с.