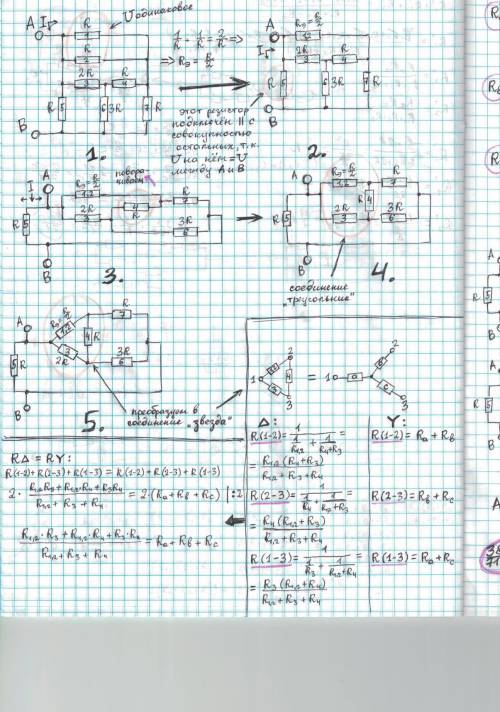
ответ - в сканах. На самом деле через резистор 4 течёт довольно малый ток. И напряжение на нём падает на небольшую величину. Сопротивление этого резистора можно сделать сколь угодно большим (чем больше его сопротивление, тем меньше сила тока в нём) - общее сопротивление цепи особо не изменится. Его даже можно убрать из расчётов - тогда преобразовывать треугольник в звезду будет уже не нужно. Это если надо высчитать сопротивление цепи. Но если надо знать какие токи будут течь в определённых участках, какими будут падения напряжения на них, то этот резистор нужно учитывать при расчётах.
Также, вместо треугольника резисторов R1,2, R4 и R3 в звезду можно преобразовать треугольник резисторов R4, R6 и R7.

Дано: t1=0∘ C, V2=2V1, ΔT−? Решение задачи: Автор задачи подразумевает, что над газом производят изобарный процесс (p=const). Это далеко не очевидно, но не зная этого, решить задачу не получится. Запишем закон Гей-Люссака: V1T1=V2T2 Тогда конечная температура газа T2 равна: T2=T1V2V1 По условию объем газа увеличивается вдвое (V2=2V1), поэтому: T2=T12V1V1=2T1 Изменение температуры газа ΔT равно: ΔT=T2–T1 ΔT=T2–T1=2T1–T1=T1 Получается, что искомое изменение температуры ΔT равно начальной температуре газа, выраженной в Кельвинах (и только в них, поскольку результат был получен из закона Гей-Люссака, в котором температура фигурирует в абсолютной шкале). Переведём температуру T1 в абсолютную шкалу температур: 0∘C=273К ΔT=273К=273∘С Изменение температуры одинаково, что выраженная в Кельвинах, что и в градусах Цельсия. ответ: 273 °С.
R = R1 + R2
R = 20 Ом
I = U/R
I = 1 A
Q1= I²R1t Q1 = 125 Дж
Q2 = I²R2t Q2= 375 Дж