Так как об ускорении в условии ни слова, принимаем движение бруска за равномерное.
Дано:Первое время движения: t₁ = 1 c.
Путь за первое время: S₁ = 50 см = 0,5 м.
Второе время движения: t₂ = 2 c.
Найти нужно путь за второе время: S₂ - ?
Решение:1. Так как движение равномерное, скорость будет одинакова как для первого участка, так и для второго, V₁ = V₂ = V.
2. Формула пути равномерного движения: 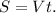
3. Выразим скорость из (2) для первого участка: 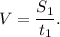
4. Применим формулу (2) для второго участка, зная, что скорость на нём такая же, как и на первом, т. е. (3): 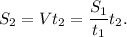
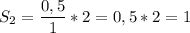 (м).
(м).
Решение задачи предусматривет знание правила рычага (во сколько раз мы выигрываем в силе во столько раз мы проигрываем в расстоянии и - наоборот).
А также знание формулы по которой определяется такая физическая величина как РАБОТА.
А=FxH
То есть работа равна произведению силы F и расстояния Н , на которое переместилось тело ( нашем случае - поршень).
Если учитывать что малый и большой поршень совершили одинаковую работу , то можно составить уравнение
F1xH1=F2xH2 , где F1=500 Hьютонов -сила действующая на малый поршень
Н1= 0,1 М - перемещение малого поршня
F2=X - искомая сила , действующая на большой поршень
Н2= 0,25М - перемещение большого поршня
500х0,1=Хх0,25
И все реши уравнение
Дано m=5 кг F=20 Н t=2 с Рx-? P-?
1 вдоль оси ох
а=F/t a=20/5=4 м/с V=Vo+a*t=6+8=14 м/с Px=m*Vx=5*14 =70 кг*м/с
2 вдоль OY a (Y)= 4м/с Vy=8 м\с
по теореме Пифагора V = корень из 64 +36=10 м/с
Р2= m*V=5*10 =50 кг*м/с