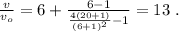– длина одного вагона или локомотива,
– длина одного вагона или локомотива,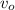 – скорость передней точки локомотива, когда он проезжает мимо,
– скорость передней точки локомотива, когда он проезжает мимо,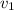 – скорость поезда, когда локомотив только что проехал наблюдателя,
– скорость поезда, когда локомотив только что проехал наблюдателя, – скорость поезда, когда только k вагонов ещё не проехали мимо,
– скорость поезда, когда только k вагонов ещё не проехали мимо, – скорость поезда, когда весь поезд проехал наблюдателя,
– скорость поезда, когда весь поезд проехал наблюдателя,
 наступило состояние
наступило состояние 
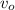 и
и  – отделаят промежуток времени
– отделаят промежуток времени 
 и
и  – очевидно отделаят промежуток времени
– очевидно отделаят промежуток времени 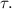
 [1]
[1]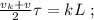 [2]
[2]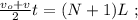 [3]
[3]
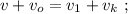 [4]
[4]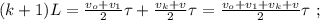
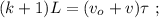
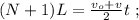
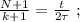
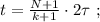 [5] – это всё время движения поезда мимо наблюдателя:
[5] – это всё время движения поезда мимо наблюдателя: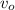 до значения
до значения 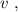 изменяясь на величину
изменяясь на величину 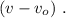
 скорость возрастёт только на величину:
скорость возрастёт только на величину: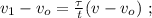
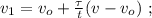

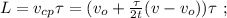 [6]
[6]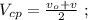
 [7]
[7]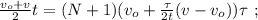
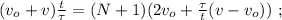
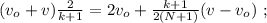


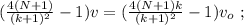
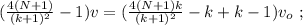


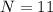 и
и 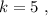 получаем:
получаем: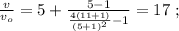
 и
и 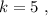 получаем:
получаем: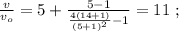
 и
и 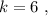 получаем:
получаем: