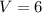 литров
литров 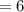 дм³
дм³  см³
см³ 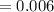 м³ ;
м³ ;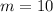 кг ;
кг ;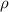 ;
;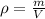 ;
;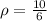 кг/л
кг/л 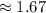 кг/л ;
кг/л ;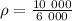 г/см³
г/см³ 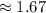 г/см³
г/см³ 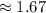 г/мл ;
г/мл ;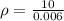 кг/м³
кг/м³ 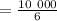 кг/м³
кг/м³ 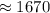 кг/м³ ;
кг/м³ ;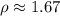 кг/л
кг/л 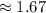 г/см³
г/см³ 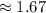 г/мл
г/мл 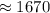 кг/м³ .
кг/м³ .Дано: v = 15*10⁻⁶ м³ ρ = 2700 кг/м³ ρ₁ = 1000 кг/м³ g = 10 н/кг найти: f - ? допустим, что в качестве камня рассматривается гранит с плотностью ρ = 2700 кг/м³ тогда вес камня (сила тяжести, действующая на камень): p = fт = mg = ρvg = 2700*15*10⁻⁶*10 = 0,405 (h) на камень, погруженный в воду действует выталкивающая сила, численно равная весу воды в объеме камня: fa = ρ₁gv = 1000*10*15*10⁻⁶ = 0,15 (h) сила, которую надо приложить к камню, чтобы удержать его в воде: f = p - fa = 0,405 - 0,15 = 0,255 (h) ответ: 0,255 н.
Объяснение:
Под средней длиной свободного пробега понимают среднее расстояние, которое проходит молекула между двумя последовательными соударениями. за секунду молекула в среднем проходит расстояние, численно равное ее средней скорости . если за это же время она испытает в среднем столкновений с другими молекулами, то ее средняя длина свободного пробега , очевидно, будет равна (3.1.1) предположим, что все молекулы, кроме рассматриваемой, неподвижны. молекулы будем считать шарами с диаметром d. столкновения будут происходить всякий раз, когда центр неподвижной молекулы окажется на расстоянии меньшем или равном d от прямой, вдоль которой двигается центр рассматриваемой молекулы. при столкновениях молекула изменяет направление своего движения и затем движется прямолинейно до следующего столкновения. поэтому центр движущейся молекулы ввиду столкновений движется по ломаной линии (рис. 1). рис. 1 молекула столкнется со всеми неподвижными молекулами, центры которых находятся в пределах ломаного цилиндра диаметром 2d. за секунду молекула проходит путь, равный . поэтому число происходящих за это время столкновений равно числу молекул, центры которых внутрь ломаного цилиндра, имеющего суммарную длину и радиус d. его объем примем равным объему соответствующего спрямленного цилиндра, т. е. равным если в единице объема газа находится n молекул, то число столкновений рассматриваемой молекулы за одну секунду будет равно (3.1.2) в действительности движутся все молекулы. поэтому число столкновений за одну секунду будет несколько большим полученной величины, так как вследствие движения окружающих молекул рассматриваемая молекула испытала бы некоторое число соударений даже в том случае, если бы она сама оставалась неподвижной. предположение о неподвижности всех молекул, с которыми сталкивается рассматриваемая молекула, будет снято, если в формулу (3.1.2) вместо средней скорости представить среднюю скорость относительного движения рассматриваемой молекулы. в самом деле, если налетающая молекула движется со средней относительной скоростью , то молекула, с которой она сталкивается, оказывается покоящейся, что и предполагалось при получении формулы (3.1.2). поэтому формулу (3.1.2) следует написать в виде: (3.1.3) предположим, что скорости молекул до столкновения были и тогда из треугольника скоростей имеем (рис. 2) (3.1.4) так как углы и скорости и , с которыми сталкиваются молекулы, очевидно, являются независимыми случайными величинами, то среднее рис. 2 от произведения этих величин равно произведению их средних. поэтому (3.1.5) с учетом последнего равенства формулу (3.1.4) можно переписать в виде: (3.1.6) так как cредняя квадратичная скорость пропорциональна средней скорости, (3.1.7) т. е. .поэтому соотношение (3.1.6) можно представить так: (3.1.8) с учетом последнего выражения формула для средней длины свободного пробега приобретает вид: (3.1.9) для идеального газа . поэтому (3.1.10) отсюда видно, что при изотермическом расширении (сжатии) средняя длина свободного пробега растет (убывает).как было отмечено во введении, эффективный диаметр молекул убывает с ростом температуры. поэтому при заданной концентрации молекул средняя длина свободного пробега увеличивается с ростом температуры. вычисление средней длины свободного пробега для азота (d = 3•10-10 м), находящегося при нормальных условиях (р = 1,01•105 па, т = 273,15 к) дает: , а для числа столкновений за одну секунду: . таким образом, средняя длина свободного пробега молекул при нормальных условиях составляет доли микрон, а число столкновений – несколько миллиардов в секунду. поэтому процессы выравнивания температур (теплопроводность), скоростей движения слоев газа (вязкое трение) и концентраций (диффузия) являются достаточно медленными, что подтверждается опытом.
a=V-Vo/t
-0,6=0-Vo/20
Vo=0,6 x 20= 12
ускорение -0,6, так как автомобиль не разгоняется, а тормозит, что нибудь ещё не понятно? спрашивай, я подскажу