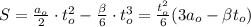Физика: На какой глубине в керосине давление 100 паскалей.

На какой глубине в керосине давление 100 паскалей.

👇

Увидеть ответ

Ответ:

ааааннннгггшим

14.09.2020

P=p(плотность)*g*h где h-глубина
h=P/(p*g)=100/(900*10)=1/90 м

4,4(35 оценок)

Открыть все ответы

Ответ:

myrzik5293p081ps

14.09.2020

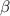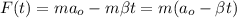$S = \frac{a_o}{2} \cdot t_o^2 - \frac{\beta}{6} \cdot t_o^3 = \frac{t_o^2}{6} ( 3 a_o - \beta t_o )$ , где $\beta$ параметр уравнения: $F(t)=ma_o-m\beta t=m ( a_o - \beta t )$ .

Считя, что сила в конце заданного интервала времени угасает полностью, мы получаем дополнительный краевой критерий и параметр 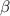$\beta$ вычисляется, при этом:

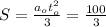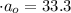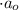$S = \frac{a_ot_o^2}{3} = \frac{100}{3}$ сек² $\cdot a_o = 33.3$ сек² $\cdot a_o$ ;

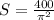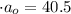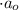*** гармоническое решение: $S = \frac{400}{\pi^2}$ сек² $\cdot a_o = 40.5$ сек² $\cdot a_o$ .

Объяснение:

Силу, действующую на материальную точку, можно выразить линейной функцией:

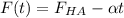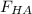$F(t)=F_{HA}-\alpha t$ , где $F_{HA}$ – начальная сила.

Ускорение:

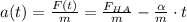$a(t) = \frac{F(t)}{m} = \frac{F_{HA}}{m} - \frac{\alpha}{m} \cdot t$ ;

Обозначим: 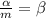$\frac{\alpha}{m} = \beta$ и, поскольку: 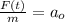$\frac{F(t)}{m} = a_o$ , то:

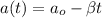$a(t) = a_o - \beta t$ ;

Интегрируем для скорости:

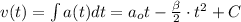$v(t) =\int a(t)dt = a_o t - \frac{\beta}{2} \cdot t^2 + C$ ;

Из начальных условий:

v(0) = C = 0 ;

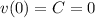Тогда:

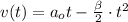$v(t) = a_o t - \frac{\beta}{2} \cdot t^2$ ;

Интегрируем для координаты:

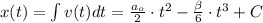$x(t) = \int v(t)dt = \frac{a_o}{2} \cdot t^2 - \frac{\beta}{6} \cdot t^3 + C$ ;

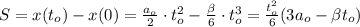$S = x(t_o)-x(0) = \frac{a_o}{2} \cdot t_o^2 - \frac{\beta}{6} \cdot t_o^3 = \frac{t_o^2}{6} ( 3 a_o - \beta t_o )$ ;

Мы не знаем величину 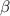$\beta$ . Если предположить, что в конце движения, при 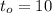t_o = 10 сек, сила 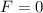F = 0 , т.е. убывает до нуля, то тогда и ускорение в конце движения тоже равно нулю:

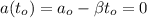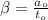$a(t_o) = a_o - \beta t_o = 0$ , и $\beta = \frac{a_o}{t_o}$ .

В таком случае:

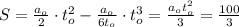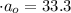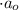$S = \frac{a_o}{2} \cdot t_o^2 - \frac{a_o}{6t_o} \cdot t_o^3 = \frac{a_ot_o^2}{3} = \frac{100}{3}$ сек² $\cdot a_o = 33.3$ сек² $\cdot a_o$ ;

*** если же равномерность убывания силы относится не ко времени, а к координате, т.е. если сила убывает раномерно с координатой, и причём до нуля, то тогда это движение будет носить гармонический характер в течении четверть периода убывания ускорения от амплитудного до нуля, т.е. при изменении фазы на 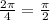$\frac{2\pi}{4}=\frac{\pi}{2}$ ;

отсюда легко найти циклическую частоту: 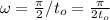$\omega = \frac{\pi}{2} / t_o = \frac{\pi}{2t_o}$ .

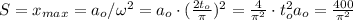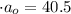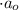для гармонического движения, верно, что ускорение софазно с координатой, т.е. на данном четверть периоде происходит и изменение координаты от амплитудного значения до нуля; стало быть, искомый путь будет равен амплитуде: $S = x_{max} = a_o / \omega^2 = a_o \cdot ( \frac{2t_o}{\pi} )^2 = \frac{4}{\pi^2} \cdot t_o^2 a_o = \frac{400}{\pi^2}$ сек² $\cdot a_o = 40.5$ сек² $\cdot a_o$ .

4,5(94 оценок)

Ответ:

mondy358

14.09.2020

1) Закрыв отверстие носика воронки, наполнили ее водой . Затем прикрыли сверху листом бумаги и, придерживая его , перевернули воронку . Отпадет ли лист бумаги? Лист бумаги не отпадет, потому что снизу на лист бумаги действует атмосферное давление, которое и удерживает лист и воду над листом.
2) Колбу с водой поставили под колокол.При откачивани воздуха из под колокола вода из колбы начнет бить фонтанчиком.Почему?
Если из под колокола начать откачивать воздух то давление под колоколом станет меньше, а давление воздуха в колбе останется прежним. Воддух в колбе давит на поверхность воды в колбе , выдавливает ее и заставляет бить фонтаном
(ответ на 5 )

4,7(30 оценок)

Это интересно:

Здоровье

03.04.2021

Как вылечить прищемленный палец: лечение дома и медицинские советы...

Семейная-жизнь

28.05.2021

Как помочь родителям, которые похоронили своего ребенка: советы и рекомендации...

Компьютеры-и-электроника

26.03.2023

Как изменить проверочный номер для кода безопасности iCloud на iPhone...

Здоровье