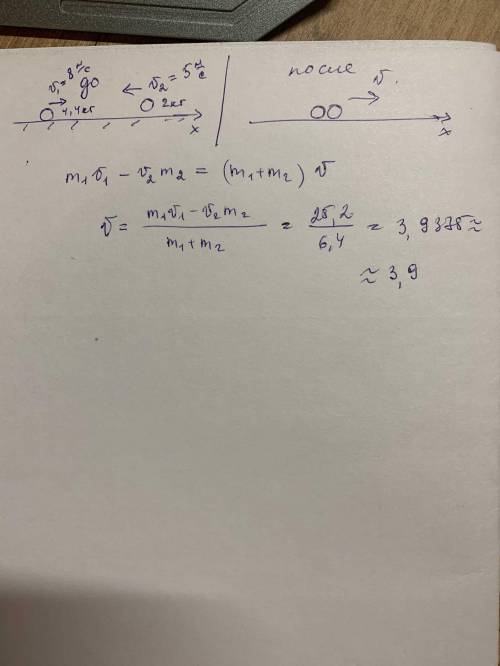
Объяснение:Два пластилиновых шарика массами m1= 4,4 кг и m2= 2 кг движутся по гладкой горизонтальной поверхности вдоль одной прямой навстречу друг другу со скоростями v1= 8 м/с и v2= 5 м/с соответственно. Через некоторое время шарики сталкиваются, склеиваются и далее начинают двигаться как одно тело. Определи скорость шариков после склеивания. (ответы округли до десятых.) Шаг 1. Найди импульс первого шарика до взаимодействия: p1= 4,4*8 кг·м/с=35,2кг·м/с. Шаг 2. Найди импульс второго шарика до взаимодействия: p2= 2*5 кг·м/с=10кг·м/с. Шаг 3. Найди суммарный импульс двух шариков до взаимодействия, учитывая, что шарики движутся навстречу друг другу: p= 35,2кг·м/с-10кг·м/с=25,2 кг·м/с.
Шаг 4. Найди массу тела, которое получается из слипшихся шариков: m= 6,4кг. Шаг 5. Обозначив скорость тела после слипания шариков как v, запиши импульс P тела после взаимодействия: (m1+m2)V=p1⋅p2 Шаг 6. Поскольку два шарика являются замкнутой системой, то для них выполняется закон сохранения импульса: импульс системы до взаимодействия равен импульсу системы после взаимодействия. Составь уравнение согласно закону сохранения импульса: (m1+m2)V=p1⋅p2 — и реши его относительно v с точностью до десятых: v = 3,9м/с.
L₁ / L₂ = 4
Объяснение:
Пусть промежуток времени равен t.
Тогда период колебаний первого маятника
T₁ = t / n₁
Второго:
T₂ = t/n₂
Найдем отношение периодов:
T₁ / T₂ = t *n₂/ t*n₁ = n₂ / n₁ = 30 / 15 = 2.
Запишем формулы периодов и снова найдем их отношение:
T₁ = 2π*√ (L₁ / g)
T₂= 2π*√ (L₂ / g)
T₁ / T₂ = √ (L₁ / L₂)
2 = √ (L₁ / L₂)
Возведем в квадрат:
4 = L₁ / L₂
Длина первого маятника в 4 раза больше длины второго маятника