Время в первом случае: t₁ = 2 c.
Кол-во колебаний: N₁ = 1.
Время во втором случае: t₂ = 8 c.
Найти нужно количество колебаний во втором случае, а также частоту колебаний маятника, то есть: N₂, υ - ?
Решение:1. Формула периода колебаний маятника: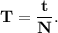 
2. Период для обоих случае одинаковый, то есть: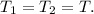 
3. Запишем (2), расписав периоды по формуле (1):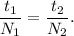 
4. Выразим количество колебаний из (3):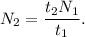 
5. Формула частоты колебаний: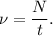 
Для вычисления частоты подойдут данные как второго так и первого случаев, считать будем так: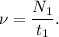 
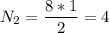(колебания).
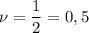(Гц).
Дано:
e₁=832· sin (ωt+35°) = 832·cos (ωt + 55°) В
e₂=675· sin (ωt+53°) = 675·cos (ωt + 37⁰) В
e₃=345· sin (ωt+60°) = 345·cos (ωt + 30°) В
e₁₂₃ - ?
1)
Сложим первые 2 колебания:
E₁₂ = √ (E₁²+E₂²+2·E₁·E₂cos(φ₁-φ₂) ) =
= √ (832²+675²+2·832·675·cos(55-37) ) ≈ 1490 В
2) Найдем фазу:
tg φ₁₂ = (E₁sin φ₁ + E₂sin φ₂) / (E₁cosφ₁ + E₂ cos φ₂) =
= (832·sin 55+675·sin37) / (832·cos 55+675·cos 37) =1,0704
φ₁₂ ≈ 45°
Получили:
e₁₂ = 1490·cos (ωt + 45°)
А теперь совершенно аналогично (как я сделал), сложи
e₁₂ = 1490·cos (ωt + 45°) и
e₃=345·cos (ωt + 30°)/.
Удачи! (Да и углы какие красивые: 30° и 45°... А мы из школы знаем синусы-косинусы этих углов)
Если не получится - пиши, проверю твои вычисления!
