Добротность (Q) резонансной цепи характеризует ее качество. Более высокое значение этого показателя соответствует более узкой полосе пропускания (что весьма желательно для многих схем). Если говорить проще, то добротность представляет собой отношение энергии, накопленной в реактивном сопротивлении цепи, к энергии, рассеиваемой активным сопротивлением этой цепи:
rezonans40
Данная формула применима к последовательным резонансным цепям, а также к параллельным резонансным цепям, если сопротивление в них включено последовательно с катушкой индуктивности. Действительно, в практических схемах нас часто беспокоит сопротивление катушки индуктивности, которое ограничивает добротность. Заметьте: Некоторые учебники в формуле "Q" для параллельных резонансных схем меняют местами X и R. Это верно для большого значения R, включенного параллельно с C и L. Наша формула верна для небольшого значения R, включенного последовательно с L.
Практическое применение добротности (Q) заключается в том, что напряжение на L или С в последовательной резонансной цепи в Q раз больше общего приложенного напряжения. В параллельной резонансной цепи ток через L или С в Q раз больше общего приложенного тока.
12 рад/с
Объяснение:
Дано:
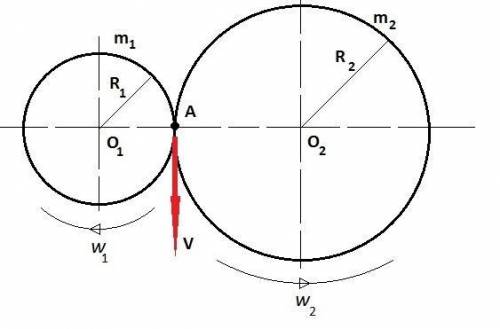
R₁ = 0,5 м
R₂ = 7,0 м
m₁ = 240 кг
m₂ = 900 кг
A = 20 кДж = 20 000 Дж
___________
ω₁ - ?
1)
Поскольку колеса находятся в зацеплении, то линейная скорость точки А равна
V = V₁ = V₂
V₁ = ω₁·R₁ (1)
V₂ = ω₂·R₂ (2)
Приравняем (2) и (1)
ω₂·R₂ = ω₁·R₁
ω₂ = (R₁/R₂)·ω₁ = (0,5/7)·ω₁ = ω₁/14
2)
Считаем зубчатые колеса тонкими обручами найдем их моменты инерции:
J₁ = m₁·R₁² = 240·0,5² = 60 кг·м²
J₂ = m₂·R₂² = 900·7² = 44 100 кг·м²
3)
Кинетические энергии колес:
T₁ = J₁·ω₁²/2 = 60·ω₁² / 2 = 30·ω₁²
T₂ = J₂·ω₂²/2 = 44 100·ω₁²/(2·14²) ≈ 110·ω₁²
Суммарная кинетическая энергия:
T = T₁+T₂ = 30·ω₁² + 110·ω₁² ≈ 140·ω₁² Дж
4)
По закону сохранения энергии:
T = A
140·ω₁² = 20 000
ω₁ = √ (20 000 / 140) ≈ 12 рад/с
Да ,они движутся относительно ровно,так как поездо едит прямолинейно