1) примеры явлений.какие из них являются примерами механических,тепловых,электрических,магнитных,звуковых,световых явлений? 2) примеры тел.назовите вещества,из которых они состоят. 3)в чем прояаляет связь между и астрономией? примеры. я у чужого компьютера мне не долго сидет буду

👇

Ответ:

exampllee1

01.01.2022

ответ на первый вопрос в скане. Я скопировал свой ответ на похожий вопрос.
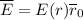
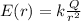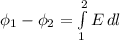
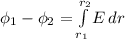
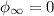
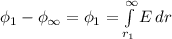
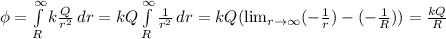
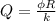
2. Физические тела - это материальные объекты, имеющие массу, объем, форму и отделенные от других тел некоей границей (поверхностью). Тема большая, поэтому вкратце. Имеются однородные тела (состоящие из одинаковых молекул или атомов, например - железо, водород, золото, вода и тд. Бывают неоднородные, составные (то есть состоящие из так или иначе скрепленных между собой простых тел. Надо осознавать, что при фазовом переходе, (например расплавление железа, или замерзание воды) физическое тело остается физическим телом.
3. Астрономия раздел науки, который некогда отделился от астрологии и занимался изучением взаимного расположения и поведения космических объектов (звезд, планет, галактик). Когда понадобилось изучать уже физические свойства этих объектов, астрономия непринужденно стала частью физики, и в некоторых областях уже сложно разделить астрономические задачи от физических. Например, изучение возраста вселенной, поведение вселенной (в том числе и прогнозируемое) после большого взрыва и так далее.

4,4(31 оценок)

Открыть все ответы

Ответ:

Polinka21a

01.01.2022

1.потенциальная энергия поднятого тела над землей переходит в кинетическую энергию движущегося тела.

после удара кинетическая энергия копра переходит в кинетическую энергию сваи, свая движется в почве под действием трения и ее кинетическая энергия переходит во внутреннюю энергию сваи и почвы.

2.кинетическая энергия движущегося автомобиля за счет трения переходит во внутреннюю энергию тормозных колодок, нагревающихся шин и дорожного покрытия.

3.вначале оба шарика потенциальной энергией, которая переходит в кинетическую энергию.

в первом случае соударение : кинетическая энергия шарика переходит в потенциальную энергию деформировавшейся плиты и шарика; а затем она снова переходит в кинетическую энергию шарика. эта кинетическая энергия затем переходит в потенциальную энергию по мере подъема шарика.

во втором случае кинетическая энергия шарика переходит во внутреннюю энергию шарика и песка.

4.кинетическая энергия шнура переходит во внутреннюю энергию шнура и трубки; затем внутренняя энергия трубки посредством теплопередачи частично переходит во внутреннюю энергию эфира. внутренняя энергия эфира при кипении эфира переходит в потенциальную энергию сжатого пара, а она, в свою очередь, переходит в кинетическую энергию пробки; по мере подъема пробки вверх ее кинетическая энергия переходит в потенциальную энергию.

4,5(94 оценок)

Ответ:

Миша3456

01.01.2022

1. Структура электростатического поля
В силу симметрии задачи, электростатическое поле является центрально-симметричны. т.е. $\overline E = E(r) \overline r_0$
r₀ - единичный радиус-вектор от заряда к произвольной исследуемой точке пространства.
Задача и её решение инвариантна к повороту (как картинку "ни крути" вокруг заряда, условие задачи и её решение не изменится).

2. Поле при отсутствии шара
Когда у нас есть только точечный заряд модуль напряженности электростатического поля $E(r) = k\frac{Q}{r^2}$ .

Потенциал электростатического поля связан с его напряженностью уравнением:
$\phi_1-\phi_2 = \int\limits^{2}_{1} {E} \, dl$
Интегрирование ведётся по произвольному пути между точками 1 и 2.

Отступление: если домножить уравнение на пробный заряд, то получим определение потенциальной энергии. Правый ингтеграл в этом случае будет работой, совершенной полем над пробным зарядом.

В нашем случае удобно интегрировать вдоль радиальных линий
$\phi_1-\phi_2 = \int\limits^{r_2}_{r_1} {E} \, dr$

Замечание: Потенциал определяется всегда с точностью до аддитивной постоянной, поэтому во всех задачах всегда выбирается, так называемое, условие нормировки. В разных задачах оно выбирается по разному, но в задачах данного типа принято брать потенциал бесконечно удаленной точки равным нулю $\phi_\infty = 0$

$\phi_1-\phi_\infty = \phi_1 = \int\limits^{\infty}_{r_1} {E} \, dr$

Подставим в эту формулу найденное поле:
$\phi = \int\limits^{\infty}_{R} {k \frac{Q}{r^2} } \, dr = kQ\int\limits^{\infty}_{R} { \frac{1}{r^2} } \, dr = kQ ( \lim_{r \to \infty} (- \frac{1}{r}) - (- \frac{1}{R} )) = \frac{kQ}{R}$
Получили известный результат. Выразим из этого результата заряд Q.
$Q= \frac{\phi R}{k}$

3. Поле при добавлении шара.
Для поиска величины напряженности воспользуемся теоремой Гаусса.
$\int {\int {E} } \, dS = 4\pi kq$
Поток вектора напряженности электростатического поля через любую замкнутую поверхность пропорционален величине свободного заряда, находящегося внутри этой поверхности.

Выберем в качестве такой поверхности сферу радиусом r. В силу структуры поля E(r) = const.
$\int {\int {E(r)} } \, dS = E(r)\int {\int {} } \, dS =E(r)*4\pi r^2 = 4\pi kq$
$E(r) = k \frac{q}{r^2}$

Теперь рассмотрим отдельные участки:
1) Участок 0 < r < 3R
$E(r) = k \frac{Q}{r^2}$
2) Участок 3R<r<4R
E(r) = 0 - электростатического поля внутри идеальных проводников не существует. Если предположить противное, то начнётся движение зарядов и это уже не статика. :)
3) Участок r > 4R
$E(r) = k \frac{4Q}{r^2}$
4Q - суммарный заряд внутри сферы радиусом r.

Аналогично рассчитаем потенциал.
$\phi' = \int\limits^\infty_R {E(r)} \, dr = \int\limits^\infty_{4R} {k \frac{4Q}{r^2} } \, dr + \int\limits^{4R}_{3R} {0} } \, dr +\int\limits^{3R}_{R} {k \frac{Q}{r^2} } \, dr = k \frac{4Q}{4R} + k \frac{Q}{R} - k\frac{Q}{3R}$

$\phi' = k \frac{5Q}{3R}$
Подставляем в это выражение найденное ранее Q и имеем:
$\phi' = \frac{5}{3}\phi = 500$

Что стоит отметить?
1) Потенциал функция непрерывная. Если знать, что подобные симметричные структуры создают поля аналогичные точечным зарядам, то задача решается в уме.
т.е. мы ищем потенциал на внешней границе шара как потенциал точечного заряда 4Q, на внутренней границе он такой же. Ищем разность потенциалов между внутренней границей и точкой A в поле точечного заряда Q. Складываем результаты.

2) Несмотря на то, что заряд 3Q на шаре поле внутри шара не создаёт, он увеличивает потенциал точек внутри полости, т.к. создаёт дополнительное поле вне шара. Потенциал - это работа по перемещению точечного заряда из бесконечности в данную точку. Больше поле вне шара - больше работа.

3) Разность потенциалов зависит только от локального поля (поля по в окрестности пути, соединяющего две точки). Сам потенциал зависит от структуры всего поля.

4,7(30 оценок)

Это интересно:

13.03.2023

Как быстро избавиться от плохого настроения: простые и эффективные советы...

Стиль-и-уход-за-собой

21.02.2023

Как заплести косу в стиле «Хвост русалки»...

Компьютеры-и-электроника

15.07.2020

Как правильно очистить экран iPhone и iPod Touch...

Дом-и-сад

17.04.2021