1. Поломка и обгорание электроприборов.
2. Воспламенение электропроводки.
3. Падение напряжения в электросети приводит к замедлению или остановке электромоторов, вызывая остановку работы предприятий.
4. Нарушение слаженной работы электропоставляющих систем.
5. Нарушения работы подземных коммуникаций при электромагнитном воздействии.
2)разноименные притягиваются, одноименные отталкиваются
3)несколько таких преобразований:
-подводимой к ней механической энергии в электрическую;1.
Ручку располагают у края двери, чтобы увеличить расстояние до оси вращения при открывании двери. Чем дальше ручка от оси вращения, тем меньшую силу понадобится приложить, чтобы создать вращающий момент и открыть дверь
3.
Дано :
Р=100 Н
F/2-?
F=P
F/2=P/2=100 H/2=50 Н
ответ:F/2=50 H
4.
Чтобы напильник при движении всегда был горизонтален при изменении точки опоры, прилагаемые силы должны все время изменяться по величине.
5.
Равновесие нарушится
6. Кнш латунная
7. действием силы тяжести
8. Да
9.Вес мальчика и вес части доски, на которой он сидит, уравновешиваются весом части доски, расположенной с другой стороны бревна./
10. Выигрыш в силе кнш
11.
Дано:
m=120кг
F=750H
КПД-?%
Fтяж=mg=120кг*10м/с2=1200H
КПД=F/Fтяж=750Р/1200Р=62,5%.
W = mgh.
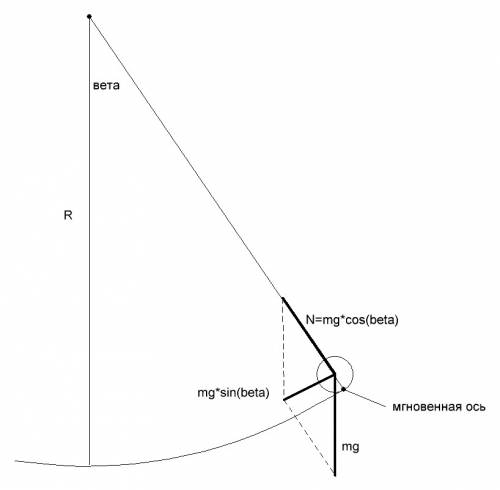
При малых смещениях можно считать, что амплитуда колебаний по дуге желоба l равна проекции этой дуги на горизонталь X0. Из прямоугольного треугольника, образованного радиусом желоба R, амплитуды горизонтального смещения X0 и проекции крайнего положения шарика на вертикаль (R-h) следует:
X0^2 + (R-h)^2 = R^2
Отсюда получим: X0^2 = 2*R*h - h^2
Учитывая, что при малых колебаниях h^2 << 2*R*h
X0^2 = 2*R*h
Таким образом, получаем выражение для h через амплитуду X0 при малых отклонениях от положения равновесия:
h = X0^2/2R
Потенциальная энергия, максимальная при крайнем положении шарика обретает вид:
W = m*g*X0^2/2R
Теперь получим значение максимальной кинетической энергии шарика (при прохождении положения равновесия). Она равна:
T = m*V0^2/2 + I*Omega^2/2
поскольку, коль шарик катится по жёлобу без проскалзывания, мы должны, помимо кин энергии поступательного движения шарика массы m, учитывать ещё и энергию вращения шарика с моментом инерции I и угловой скоростью вращения шарика вокруг его собственной оси Omega.
При этом максимальная линейная скорость шарика
V0 = Omega*r, где r = радиус шарика =>
Omega = V0/r
T = m*V0^2/2 + I*(V0/r)^2/2
Если шарик совершает гармонические колебания по закону
x(t) = X0*Sin(omega*t) то его скорость должна меняться по закону
v(t) = x'(t) = omega*X0*Cos(omega*t)
Таким образом, максимальная линейная скорость шарика (амплитуда скорости) равна
V0 = omega*X0, где omega - циклическая частота колебаний шарика.
Выражение для максимальной кинетической энергии шарика принимает вид:
T = m*(omega*X0)^2/2 + I*(omega*X0)^2/(2r^2).
Поскольку момент инерции шарика радиуса r и массы m равен
I = (2/5)mr^2, то
T = m*(omega*X0)^2/2 + (2/5)mr^2*(omega*X0)^2/(2r^2) = (7/10)m*(omega*X0)^2
В колебательной системе максимальное значение потенциальной энергии W равно максимальной величине кинетической энергии T.
(7/10)m*(omega*X0)^2 = m*g*X0^2/2R
отсюда, сокращая в обеих частях равенства m и X0 получаем:
(7/5)*omega^2 = g/R
и окончательно
omega^2 = (5/7)*(g/R)
и
omega = sqrt(5g/7R).
Частота такого "маятника" niu = omega/2Pi
niu = sqrt(5g/7R)/2Pi
Период T = 1/niu = 2Pi*sqrt(7R/5g)