m = 30 кг.
g = 10 м/с2.
а = 0 м/с2.
∠α = 30°.
μ = 0,5.
Fт - ?
Запишем 2 закон Ньютона в векторной форме для вытаскивания ящика по наклонной плоскости: m * a = Fт + m * g + N + Fтр, где Fт – сила, с которой тянут тело вверх, направленная вдоль наклонной плоскости, m * g - сила тяжести, N - сила реакции поверхности наклонной плоскости, Fтр - сила трения.
Так как по условию задачи его тянут равномерно а = 0 м/с2, то формула 2 закона Ньютона примет вид: : 0 = Fт + m * g + N + Fтр. Действие всех сил на тело скомпенсированы.
Запишем 2 закон Ньютона для проекций на координатные оси:
ОХ: 0 = Fт - Fтр - m * g * sinα.
ОУ: 0 = - m * g * cosα + N.
Fт = Fтр + m * g * sinα.
N = m * g * cosα.
Силу трения ящика о наклонную плоскость Fтр выразим формулой: Fтр = μ * N = μ * m * g * cosα.
Сила Fт, с которой тянут ящик, будет определяться формулой: Fт = μ * m * g * cosα + m * g * sinα = m * g (μ * cosα + sinα).
Fт = 30 кг * 10 м/с2 * ( 0,3 * 0,866 + 0,5) = 228 Н.
ответ: для равномерного втаскивания ящика по наклонной плоскости необходимо приложить силу Fт = 228 Н.
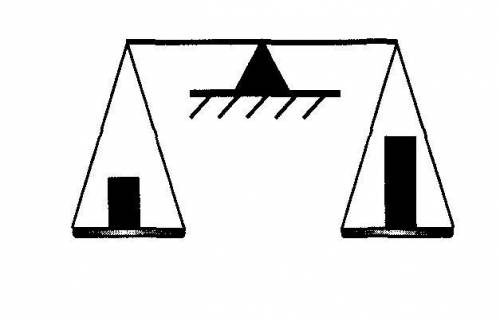
Слева брусок из свинца
Справа брусок из олова
Объяснение:
В этой задаче без рисунка не обойтись
Поэтому см. рисунок
Из рисунка мы видим то что груз который находится на равноплечих весах слева имеет меньший объём чем груз находящиеся справа но массы их должны быть одинаковы так как моменты сил которые создают оба груза равны с учётом то что весы равноплечные можем сделать вывод что их масса одинакова
Мы знаем что плотность свинца больше плотности олова и при одинаковой массе обоих тел тело из олова будет занимать больший объём нежели чем тело из свинца
F=ma=m*Δv/t
t-m*Δv/F=1.5*10^3*15/(30*10^3)=0.75 c