Виктория, задача решается так:
Дано:
Е = 200 В/м
а = 0,5 м
ε0 = 8,85•10*-12 Ф/м
Найти τ
Е = Q / 4•π•ε0•r*2 где: r - расстояние от заряда до точки наблюдения.
Q = τ•L тогда:
Е = τ•L / 4•π•ε0•r*2
Т. к. заряд Q несёт вся проволока, длину которой будем считать бесконечной, то элемент длины dL будет создавать элементарный заряд dE:
dE = [τ / 4•π•ε0•(a/cosα)*2]•dL (1)
dL = (a/cosα)•dα (2)
Подстаавим (2) в (1):
E = 2•∫[от 0 до π/2] [τ / 4•π•ε0•(a/cosα)*2]•(a/cosα)•dα (3) - в силу симметрии берётся удвоенный интеграл [от 0 до π/2], а не от [от -π/2 до π/2].
Преобразуем (3):
E = ∫[от 0 до π/2] [τ / 2•π•ε0•a]•cosα•dα = [τ / 2•π•ε0•a]• ∫[от 0 до π/2]cosα•dα
E = [τ / 2•π•ε0•a]• sinα [от 0 до π/2] = τ / 2•π•ε0•a
Откуда:
τ = 2•π•ε0•a•E
Вычислим:
τ = 2•3,14•8,85•10*-12 Ф/м • 0.5 м • 200 В/м = 5,6•10*-9 Кл/м - ответ.
Честно говоря, я даже не представляю как здесь решить по-простому. В задаче многовато неизвестных, которые в одно-два действия и не выразишь.
Дано:
h = 5 см
H = 15 см
Δd = 1,5 см
H' = 10 см
F - ?
Линзу не меняли, значит мы можем приравнять выражения для отношения (1/F) друг к другу:
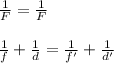 (1)
(1)d' нам известно - оно равняется расстоянию до передвижения d + изменение расстояния Δd:
d' = d + Δd
Тогда выразим f и f' из формулы линейного увеличения линзы (вместо традиционной буквы "Г" я использую букву "G", поскольку редактор уравнений не может прописывать русские буквы):

Подставляем эти выражения в уравнение (1):
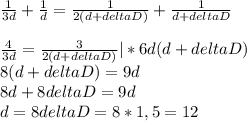
Получили значение первичного расстояния между свечой и линзой. Подставляем его в выражение для первичного расстояния f между экраном и линзой:

Возвращаемся к уравнению для обратного фокусного расстояния (1/F), переворачиваем его и подставляем найденные значения:

ответ: 9 см.
T=2π√(L/g)=0.628 c
t/T=10 периодов
Энергия меняется два раза за период
= 20 раз