Дано:
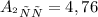 эВ
эВ
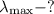
Согласно уравнению Эйнштейна для фотоэффекта энергия поглощенного кванта hν идет на совершение работы выхода A и на сообщение кинетической энергии вылетевшему электрону: 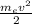
Работа выхода A - это минимальная работа, которую надо совершить, чтобы удалить электрон из металла.
Минимальная частота света v (min), при которой ещё возможен фотоэффект, соответствует максимальной длине волны λmax:

В этой формуле h – это постоянная Планка, равная 6,62·10-³⁴ Дж·с, частоту колебаний можно выразить через скорость света c, которая равна 3·108 м/с, и длину волны по формуле:
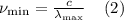
Подставим выражение (2) в формулу (1), тогда:
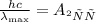
Откуда искомая красная граница фотоэффекта λmax равна:
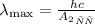
Посчитаем численный ответ (напоминаем, что 1 эВ = 1,6·10-¹⁹ Дж:
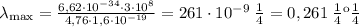
ответ: 0,261 мкм.
63 мГн
Объяснение:
Дано:
Wэ = 0,5 мДж = 0,5*10⁻³ Дж
ν = 400 кГц = 4*10⁵ Гц
qmax = 50 нКл = 50*10⁻⁹ Кл
L - ?
Запишем формулу Томсона:
T = 2π*√ (L*C)
Возведем обе части в квадрат:
T² = 4*π²*L*C
Отсюда индуктивность катушки:
L = T² / (4*π²*C) (1)
Итак, нам надо знать период T и емкость конденсатора С.
1) Период колебаний:
T = 1 / υ = 1 / 4*10⁵ = 2,5*10⁻⁶ c
2)
Емкость конденсатора найдем из формулы:
Wэ = q² / (2*C)
C = q² / (2*Wэ) = (50*10⁻⁹)² / (2*0,5*10⁻³) = 2,5*10⁻¹² Ф
3)
Найденные величины подставляем в формулу (1)
L = T² / (4*π²*C) = (2,5*10⁻⁶ )² / (4*3,14²* 2,5*10⁻¹²) ≈ 0,063 Гн или 63 мГн