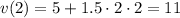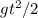
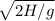
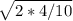=0,89c
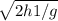, где h1=3м
=0,77c
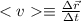
, т.е., при 
, получаем: 
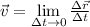
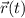по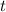 
. Величину в левой части называют мгновенной скоростью. Таким образом,
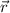в рамках данной задачи можно со спокойной душой заменить на 
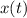, так как движение совершается вдоль прямой. Находим производную в точке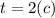 
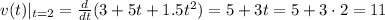
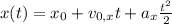и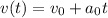 
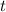., а ускорение - это удвоенный коэффициент перед 
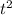, и подставляем это во второе:
