
Из первого уравнения находим время падения, а затем из второго - конечную скорость:
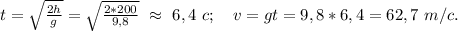
ответ: 6,4 с; 62,7 м/с.
Припасы
Всё лето геологи искали в тайге алмазы. Пришла осень. Начались дожди. Геологи стали собираться домой. Перед отъездом завхоз сообщил начальнику экспедиции, что осталось сто банок сгущёнки, три килограмма муки, мешок компота и ящик масла.
– Надо поставить склад-хранилище, – решил начальник.
Геологи взяли топоры, пилы и за три дня срубили хранилище. Склад получился вроде небольшой избушки без окон, с бревенчатыми стенами. Он был поставлен на четырёх тонких столбах так, чтобы медведь по ним не мог залезть в хранилище. Получился склад, как избушка на курьих ножках.
Уложили геологи припасы и убрали лестницу. Геологи ушли, а избушка осталась стоять в тайге.
Весной геологи вновь вернулись в тайгу искать алмазы, но расположились на другой стороне реки. Завхоз предложил молодому геологу Проньке сходить и принести ребятам сладенькой сгущёнки.
Пронька взял мешок, ружьё и отправился к старому хранилищу. Пронька шёл и свистел в костяной свисток – дразнил весенних рябчиков.
Вот и знакомое место. В груди у Проньки похолодело, а в голове вдруг стало очень горячо. Под избушкой стоял огромный бурый медведь. Передними лапами он расшатывал столб. В раскрытой двери что-то зашевелилось. Оттуда сам собой стал вылезать мешок муки. Медведь подхватил мешок, когтём продырявил дырку, поднял его и стал вытряхивать муку себе на голову. Вмиг он стал похож на огромный жёлтый одуванчик. Языком он хватал мучное облако и облизывался.
Из открытой двери склада вновь высунулась рука в лохматой варежке и бросила вниз банку сгущёнки. Медведь ловко подхватил её и с силой сдавил. Липкая сладкая масса полилась на язык медведицы. В это время ловко спустился медвежонок и подхватил банку с молоком. Он лизал её, словно сплющенный леденец.
Пронька отошёл в сторону и с другой стороны подошел к медведям. Он поднял ружьё вверх и дважды выстрелил. Не успел заглохнуть выстрел, Пронька принялся кричать, громко смеяться, звать несуществующих друзей, он даже запел. Голос его звучал хрипло, но он отыскал лестницу и приставил ее к складу. Он разыскал муку, сгущёнку, чернослив, сухие груши и яблоки, сложил всё в сумку.
Слез Пронька на землю и подобрал сплющенную банку сгущёнки, похожую на блин. Теперь нужно поскорее уходить, и Пронька запел ещё громче...
(По Ю.И. Ковалю)
Задания к тексту
7. Для чего Пронька начал кричать, смеяться, звать несуществующих друзей, когда увидел медведей?
1) чтобы привлечь внимание медведей
2) чтобы его услышали люди, которые находились поблизости
3) чтобы испугать медведей
4) чтобы повеселиться
8. Выпишите предложение, подтверждающее то, что медведи съели не все припасы.
9. Восстанови порядок описанных событий. Пункт с цифрой 1 – начало рассказа.
1) Путешествие за припасами
2) Приезд экспедиции через год
3) 1. Конец первой экспедиции
4) Встреча с медведями
5) Постройка хранилища
10. Какие слова подходят для замены выражения «мучное облако».
1) белое облако
2) рассыпавшаяся мука, летающая в воздухе
3) туман
4) мутное облако
11. Что подразумевается под выражением «рука в лохматой варежке».
1) медвежья лапа в муке
2) большая лапа
3) мохнатая лапа
4) мягкая рука
12. Как ты понимаешь выделенное выражение в предложении: «Получился склад, как избушка на курьих ножках».
1) очень старым
2) деревянным, вместительным
3) высоким, на подпорках
4) с печкой и трубой
13. Определи жанр этого произведения:
1) сказка
2) басня
3) художественный рассказ
4) исторический рассказ
5) научно-познавательный рассказ
14. Что нужно для того, чтобы сохранить
Объяснение:
Сила давления блока на ось дF→д=−N→. где N→ — сила реакции оси, действующая на блок и направленная вверх. Кроме этой силы на блок действуют силы натяжения нити T→1, и T→2, направленные вниз. Уравнение второго закона Ньютона для блока имеет вид блцблmблa→ц=N→+T→1+T→2+mблg→, где цa→ц — ускорение центра масс блока относительно Земли, блmбл — его масса. Если блmбл→0, то независимо от ускорения центра масс N→+T→1+T→2=0,N=T1+T2.
Таким образом, задача сводится к нахождению сил натяжения нити. Поскольку нить связывает заданные грузы, то силы натяжения могут быть найдены из рассмотрения движения грузов. При равномерном движении лифта можно выбрать систему отсчета, связанную как с Землей, так и с лифтом. При ускоренном движении лифта система отсчета, связанная с лифтом, неинерциальная, поэтому она должна быть связана с Землей. Задачу можно решить сразу для ускоренного движения лифта, а первый случай получится как частное решение при a0=0. Грузы движутся относительно блока (относительно лифта) и участвуют в движении лифта с ускорением a→0. Если нить нерастяжима, то ускорения грузов относительно блока одинаковы по модулю, но противоположны по направлениям. Для доказательства запишем условия нерастяжимости нити. Введем ось O′η, связанную с лифтом (рис.), координаты обоих тел η1, и η2. Тогда условие нерастяжимости нити η1+η2+l0=const
где l0 — длина части нити, соприкасающейся с блоком. При движении грузов относительно лифта координаты η1 и η2 изменяются, но η˙1+η˙2=0,η¨1+η¨2=0 (1) (точка над буквой обозначает производную по времени); η˙r=a1η′ — проекция ускорения первого груза относительно лифта на вертикальную ось O′η;η¨2=a2η′ - проекция ускорения второго груза на ту же вертикальную ось. Из соотношения (1) найдем a1η′=−a2η′. Поскольку грузы движутся вдоль оси O′η, то a→1′=−a→2′. Относительно Земли ускорения грузов a→1=a→+a→1′,a→2=a→0+a→2′. Каждый из грузов движется под действием силы тяжести и силы натяжения нити. Невесомость нити позволяет считать силу натяжения вдоль нити постоянной по модулю. Неизменяемость силы натяжения по модулю при переходе через блок может быть доказана при условии, что массой блока можно пренебречь. Таким образом, T1=T1′=T2=T2′. Уравнения второго закона Ньютона, записанные в скалярном виде для каждого из тел, составят систему, в которой неизвестными будут силы натяжения нити и относительные ускорения грузов. Коллинеарность сил, действующих на каждый из грузов, позволяет записать уравнения движения сразу в скалярной форме для проекций на ось OY. Для первого груза a1y=a0+a′,m1(a0+a′)=T−m1g; (2) для второго груза a2y=a0−a′,m2(a0−a′)=T−m2g, (3)
h=200 м
t,v=?
h=gt²/2
g≈10 м/с²
200=10t²/2
400=10t²
t²=40
t=√40=2√10 с≈6,3 с
g=v/t
10=v/2√10
v=20√10 с≈63,2 м/с²