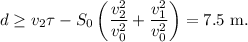Объяснение:
Длина линии, вдоль которой движется тело - это пройденный телом путь.
Длина линии,вдоль которой движется тело -это пройденный телом путь .
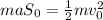
 - ускорение торможения,
- ускорение торможения, 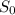 - тормозной путь (который в конце условия),
- тормозной путь (который в конце условия), 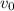 - начальная скорость (которая в конце условия).
- начальная скорость (которая в конце условия). .
.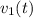 и
и  .
.
 - тормозной путь первого автомобиля,
- тормозной путь первого автомобиля, 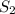 - тормозной путь второго автомобиля.
- тормозной путь второго автомобиля.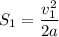 и
и 
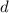 , найдем:
, найдем: