1 в
Объяснение:
Температура однородного медного цилиндрического проводника длинной 10м в течении 57 с повысилась на 10К. Определить напряжение, которое было приложено к проводнику в это время. Изменением сопротивления проводника и рассеянием тепла при его нагревании пренебречь
L=10 м
t=57 c
∆T= 10 K
U- ?
РЕШЕНИЕ
Количество тепла выделенное проводником по з-ну Дж-Ленца
Q1=U^2/R *t (1)
Сопротивление проводника длиной L
R=λL/S (2)
λ-удельное электрическое сопротивление меди =0.017 Ом*мм2/м=0.017*10^-6 Ом*м
S –поперечное сечение проводника
L-длина проводника
Подставим (2) в (1)
Q1=U^2/( λL/S) *t = U^2*S*t/( λL) (3)
Количество тепла полученное проводником от работы тока
Q2=сm∆T=cVp∆T=cLSp∆T (4)
С-удельная теплоемкость меди =400 Дж/кг*К
m-масса проводника
V-объем проводника
р-плотность меди =8920 кг/м3
по условию задачи потерь тепла нет, тогда
Q1=Q2
Приравняем (3) и (4)
U^2*S*t/( λL)= cLSp∆
U^2 =1/t *( cLp∆T)*( λL)=1/t *c λ p L^2*∆T
U=√(1/t *c λ p L^2*∆T)= √(1/57*400*0.017*10^-6*8920*10^2*10) = 1 В
ответ напряжение 1 В
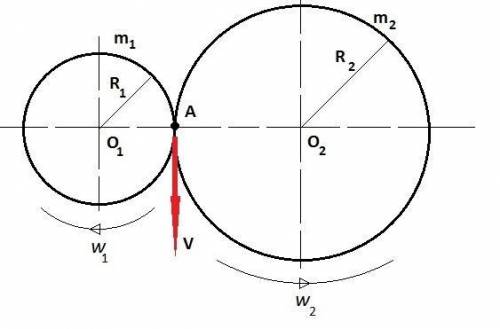
12 рад/с
Объяснение:
Дано:
R₁ = 0,5 м
R₂ = 7,0 м
m₁ = 240 кг
m₂ = 900 кг
A = 20 кДж = 20 000 Дж
___________
ω₁ - ?
1)
Поскольку колеса находятся в зацеплении, то линейная скорость точки А равна
V = V₁ = V₂
V₁ = ω₁·R₁ (1)
V₂ = ω₂·R₂ (2)
Приравняем (2) и (1)
ω₂·R₂ = ω₁·R₁
ω₂ = (R₁/R₂)·ω₁ = (0,5/7)·ω₁ = ω₁/14
2)
Считаем зубчатые колеса тонкими обручами найдем их моменты инерции:
J₁ = m₁·R₁² = 240·0,5² = 60 кг·м²
J₂ = m₂·R₂² = 900·7² = 44 100 кг·м²
3)
Кинетические энергии колес:
T₁ = J₁·ω₁²/2 = 60·ω₁² / 2 = 30·ω₁²
T₂ = J₂·ω₂²/2 = 44 100·ω₁²/(2·14²) ≈ 110·ω₁²
Суммарная кинетическая энергия:
T = T₁+T₂ = 30·ω₁² + 110·ω₁² ≈ 140·ω₁² Дж
4)
По закону сохранения энергии:
T = A
140·ω₁² = 20 000
ω₁ = √ (20 000 / 140) ≈ 12 рад/с