
Переведём данные величины сопротивления в СИ:
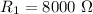 (Ω = Ом, просто в таком варианте написания нет путаницы с метрами)
(Ω = Ом, просто в таком варианте написания нет путаницы с метрами)
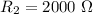
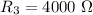
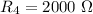
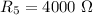
Так как у нас смешанное соединение, то нам придётся посчитать полное сопротивление цепи для расчёта остальных характеристик.
Резисторы 1 и 2 соединены параллельно, а значит 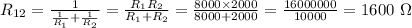
Резисторы 4 и 5 соединены последовательно, отсюда 
Резисторы 3 и 45 соединены параллельно, тогда 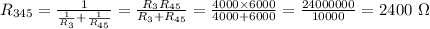
Участки цепи с резисторами 12 и 345 соединены последовательно, а значит полное сопротивление цепи 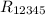 или
или 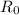 будет считаться так:
будет считаться так:
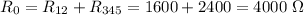
По закону Ома 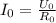 , где
, где 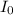 - сила тока в цепи,
- сила тока в цепи, 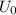 - общее напряжение
- общее напряжение
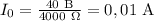
Так как участки цепи с резисторами 12 и 345 соединены последовательно, то 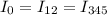 .
.
Так как резисторы 1 и 2 соединены параллельно, то 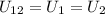
Считаем 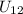 :
:
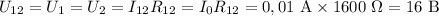
Тогда найдём силы тока для каждого из резисторов 1 и 2:
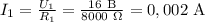
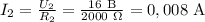
Найдём 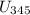 :
:
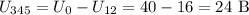
Так как резисторы 3 и 45 соединены параллельно, то 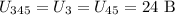
Найдём 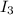 :
:
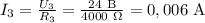
Найдём 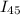 :
:
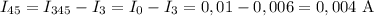
Резисторы 4 и 5 соединены последовательно, тогда 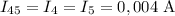
Найдём 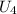 и
и 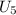 :
:
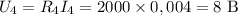
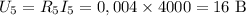
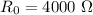 ,
, 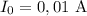 ,
, 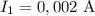 ,
, 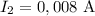 ,
, 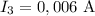 ,
, 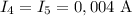 ,
, 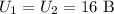 ,
, 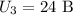 ,
,  ,
, 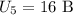
— Электроды, видимо, по площади равны площадям граней кубика: S = L² = 0,0036 м². Они образуют плоский конденсатор с емкостью С = ε°εS/d, где ε° — электрическая постоянная (См. Рис. ).
— Этот конденсатор «соединён» параллельно с активным сопротивлением R диэлектрического кубика. Оно состоит из двух “последовательно соединенных частей — R1 (объемной) и R2 (поверхностной — на 2-х контактах с электродами).
— R1 = ρ*L/L² = ρ/L; R2 = 2*σ*L².
— R = R1 + R2.
— Частота ω напряжения: ω = 2пf.
— Ёмкостное сопротивление Х (с) = 1/(ωС) = 1/(2пf*C).
— Z(R,C) = √ { R² + (X(c))² } .
— Проводимость обратно пропорциональна сопротивлению: Σ = 1/Z(R,C).
Объяснение: