1). Из условия задачи трактор находился в пути 1 час 30 минут + 30 минут + 1 час = 3 часа, включая вынужденную остановку; 2). Всего трактор преодолел 57 км = 30 км + 27 км, при чем два отрезка пути с различной скоростью; 3). Тогда, 57 км : 3 часа = 19 км/час - средняя скорость трактора на всём протяжении пути. В условии задачи не случайно указано время остановки 30 минут, которое тоже включается в общее время потраченное на всю дорогу. ответ: средняя скорость трактора на протяжении всего участка пути - 57 км составляет 19 км/час.
Переведём скорость в м/с, для этого надо км/ч разделить на 3,6. v=54/3.6=15 м/с. m=2000 кг. кинетическая энергия автомобиля перед торможением была равна E=0.5mv^2; После остановки она равнялась нулю. Чтобы остановить автомобиль, сила трения должна была совершить работу, равную этой энергии A=E. Работа равна силе трения, умноженной на тормозной путь A=F*L. Коэффициент трения k равен отношению силы трения F=A/L к силе тяжести F1=mg; k=F/F1; k=A/(Lmg); k=0.5mv^2/(Lmg); k=0.5v^2/(Lg); Нам неизвестна длина тормозного пути L. Её найдём из уравнения движения автомобиля с ускорением a=v/t; a=15/3=5 м/с^2; уравнение движения: x=vt-0.5at^2; подставляем значения скорости, ускорения и время t=3. L=15*3-0.5*5*9=45-22.5=22.5 м k=0.5*15^2/(22.5*10)=0.5; В начале торможения импульс равнялся p0=mv; p0=15*2000=30000 кг*м/с. В конце торможения импульс равен нулю, значит изменение импульса равно p0=30000 кг*м/с.
h =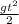
, отсюда
t =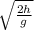
, откуда видно что t = 3 сек