Вопросы лабораторной работы: 1. при каком условии возникает индукционное электрическое поле? 2. как зависит величина индукционного тока от скорости движения магнита? 3. почему при приближении и удалении полосового магнита стрелка гальванометра откланяется в разные стороны? 4.почему при включении и выключении вторичной катушки наблюдается кратковременный индукционный ток в первичной катушке? 5. почему в первичной катушке на возникает индукционный ток, если во вторичной катушке ток имеет постоянное значение? 6. для каждого опыта объясните причины, по которым возникает индукционный ток. 7. предложите свои получения индукционного тока.

👇

Ответ:

emkaemkovich902

19.08.2020

1) Переменное магнитное поле вызывает появление вихревого( индукционного) электрического поля
3) Согласно правилу Ленца
2) Чем быстрее движется магнит, тем быстрее изменяется магнитное поле, тем больше индукционный ток.4) В момент включения ток в катушке возрастает постепенно, что вызывает переменное магнитное поле- а оно индукционный ток.5) Постоянный ток не может вызывать переменное магнитное поле, а только оно вызывает индукционный ток 6) Нет описания опытов 7) Рамка вращается в магнитном поле. катушка движется относительно магнита.

4,7(89 оценок)

Открыть все ответы

Ответ:

32519

19.08.2020

M = 5*10⁴ кг
l = 0,12 м
r = 0,1 м
Q?
Обозначим угол между нитями α, тогда sin(α/2) = (r/2) :
l = 5/12 = 0,42 (25°)
Fк+mg+T=0
x: Fк - T*sin(α/2) = 0 ⇒ Fк = T*sin(α/2) (1)
y: -mg+T*cos(α/2) = 0 ⇒ T = mg/cos(α/2) (2)
Подставим (2) в (1): Fк = mg*sin(α/2)/cos(α/2) = mg*tg(α/2) (3)
[arctg25° = 0,47]
Fк = Q²/4πε₀*r² (4)
Приравняем (3) и (4): Q²/4πε₀*r² = mg*tg(α/2) ⇒
Q = 2r*√(πε₀*mg*tg(α/2))
Q = 2*0,1√(3,14*8,85*10^-12*5*10^-4*9,8*0,47) =
= 0,2*25,2*10^-8 = 5*10^-8 Кл
|Q| = 5*10^-8 Кл

4,6(35 оценок)

Ответ:

mrkrbnv

19.08.2020

Либо я что-то не так понимаю, либо задачка совсем непростая.
Пусть

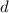- прицельный параметр (его мы и будем искать потом).
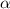Легко видеть, что направление скорости мишени после удара не зависит от скорости налетающего шара и составляет угол $\alpha$ с горизонтом такой, что его синус 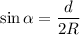$\sin \alpha=\dfrac{d}{2R}$ , где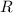

- радиус каждого из шаров.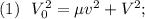
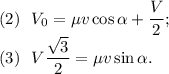
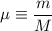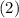Пишем теперь законы сохранения:
энергии:
$\mathrm{(1)\ \ }V_0^2=\mu v^2+V^2;$
импульса:
$\mathrm{(2)\ \ } V_0=\mu v\cos\alpha+\dfrac{V}{2};\\ \mathrm{(3)\ \ } V\dfrac{\sqrt3}{2}=\mu v\sin\alpha.$
(Здесь принято обозначение $\mu\equiv\dfrac mM$ .)
Теперь делаем такой трюк: выразим из уравнений (2)

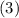члены, содержащие выражения с фактором 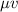$\mu v$ , возведем их в квадрат и сложим. Тогда около этого фактора после сложения окажется тригонометрическая единица. Так мы избавляемся от функции угла.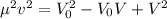
$\mu^2v^2=V_0^2-V_0V+V^2$
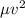Отсюда возьмем $\mu v^2$ и подставим эту конструкцию в (1)

.
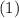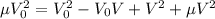$\mu V_0^2=V_0^2-V_0V+V^2+\mu V^2$ .
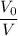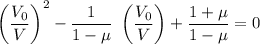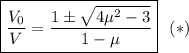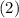Это квадратное уравнение относительно $\dfrac{V_0}{V}$ :
$\left(\dfrac{V_0}{V}\right)^2-\dfrac{1}{1-\mu}\ \left(\dfrac{V_0}{V}\right)+\dfrac{1+\mu}{1-\mu}=0$ .
Его решение имеет вид:
$\boxed{\dfrac{V_0}{V}=\dfrac{1\pm\sqrt{4\mu^2-3}}{1-\mu}}\ \ \mathrm{(*)}$ .
Теперь вспоминаем про функцию угла, содержащуюся в уравнениях (2)

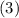. Опять выражаем из них выражения с фактором 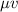$\mu v$ , но в этот раз мы разделим одно на второе (косинус на синус, например). Получим: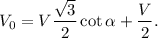
$V_0=V\dfrac{\sqrt3}{2}\cot\alpha+\dfrac V2.$
Другими словами,
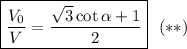$\boxed{\dfrac{V_0}{V}=\dfrac{\sqrt3 \cot\alpha+1}{2}}\ \ \mathrm{(**)}$ .
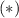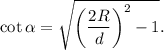
Сравнивая $\mathrm{(*)}$ и $\mathrm{(**)}$ , находим одно тривиальное решение, отвечающее отсутствию удара вообще и одно нетривиальное, отвечающее равенству правых частей. Это равенство представляет из себя некое уравнение на угол. Теперь мы вспомним про самое первое уравнение, написанное в решении. Из него легко получить $\cot\alpha=\sqrt{\left(\dfrac{2R}{d}\right)^2-1}.$
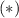Принимая это во внимание и разрешая получившееся из $\mathrm{(*)}$ и $\mathrm{(**)}$ уравнение относительно прицельного параметра, получим окончательный ответ:
$d=2R\left\{\dfrac13\left[1+\left(-1+2\dfrac{1\pm\sqrt{4\mu^2-3}}{1-\mu}\right)\right]^2\right\}^{-1/2}.$

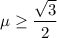Отсюда, кстати, видно условие на отношение масс: оно должно быть таким, чтобы корень был неотрицательным, т.е., необходимое условие для того, чтобы описанное в условии движение могло иметь место в принципе, выглядит следующим образом: $\mu \geq \dfrac{\sqrt3}{2}$ .