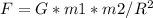Перевести в кпа следующие значения: 2500 па; 12300 па; 450 па.

Question

Физика: Перевести в кпа следующие значения: 2500 па; 12300 па; 450 па.

mixtalalai2017 · Accepted Answer

Распишем второй закон Ньютона для одного из находящихся в равновесии шаров : 0=Fвт - Fк , Где Fвт- сила всемирного тяготения ,а Fк - Сила Кулона.
Тогда чтобы шарики находились в равновесии ,нужно ,чтобы сила В.т была равна силе Кулона.Получается:
Fвт=Fк Распишем эти силы:
F=G*m1*m2/R^2

, где G-гравитационная постоянная,m1 и m2 -массы тел, R^2-квадрат расстояния между телами
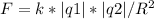F=k*|q1|*|q2|/R^2

,где k-электрическая постоянная,q1 и q2- модули зарядов, R^2-квадрат расстояния между зарядами
У нас расстояние между зарядами и шариками равно. Заряды равны. Выразим отсюда заряд:
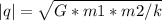$|q|= \sqrt{G*m1*m2/k$ Теперь осталось подсчитать ,что получится. Думаю,ты сам справишься!

MOGZ ответил