Объяснение:
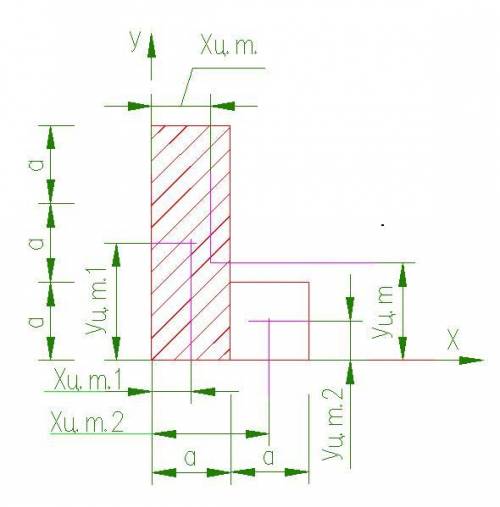
Пластина делится на две прямоугольные части.
У прямоугольника центр тяжести в середине.
У первой - заштрихованной пластины площадь 3a^2
А расстояния от координатных осей до центра тяжести:
Хцт1=0,5а
Уцт1=1,5а
У второй пластины площадь a^2
расстояния от координатных осей до центра тяжести:
Хцт2=1,5а
Уцт1=0,5а
Центр тяжести можно найти если просуммировать площади умноженные на расстояние до центра тяжести каждой простой фигуры, а потом эту сумму поделить на общую площадь.
Общая площадь фигуры 4а^2
Остается посчитать
Хц.т.=(3a^2*0,5а+a^2*1,5а)/4а^2=3а^3/4а^2=3а/4=0,75а
Уц.т.=(3a^2*1,5а+a^2*0,5а)/4а^2=3а^3/4а^2=5а/4=1,25а
Картинка приложена
Закон радиоактивного распада
тут
N(t) - число нераспавшихся частиц к моменту времени t
t - текущее время
λ - постоянная распада
Тут при решении надо выражать λ и t в одних и тех же единицах.
Период полураспада (обозначим
Из (1) и (2) следует
откуда можно выразить характерное время λ
Теперь, если подставить в (1) t=12,9 дней, λ найденное из (3), получим:
Отношение начального числа частиц
Ну теперь осталось только в (3)и (5) числа подставить
λ=ln(2)/3,8≈0,1824
Уменьшилось число частиц