 тогда мы можем выразить время, которое тратит жук на прохождение расстояния между
тогда мы можем выразить время, которое тратит жук на прохождение расстояния между 
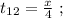
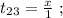
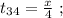


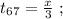
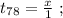

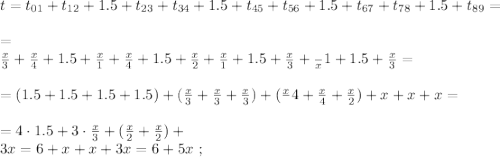


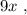 поскольку мы изначальнго определили
поскольку мы изначальнго определили  как цену деления линейки Глюка. Стало быть:
как цену деления линейки Глюка. Стало быть:
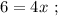
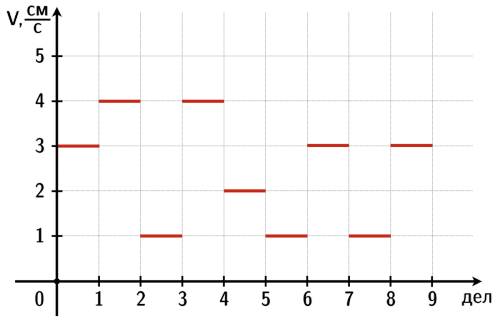
 см
см
Скорость тела 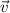 можно представить в виде векторной суммы проекций:
можно представить в виде векторной суммы проекций:
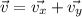
В частности для начальной скорости:
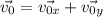
Модули проекций определяются соотношениями:
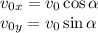
Движение по горизонтали является равномерным, то есть проекция начальной скорости на ось х не изменяется с течением времени.
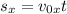
Подставляя соотношение для проекции, получим:
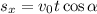
Подставляем значения:
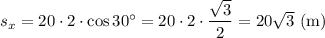
Движение по вертикали является равнопеременным. Проекция начальной скорости на ось y меняется с течением времени вследствие ускорения свободного падения.
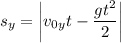
Подставляя соотношение для проекции, получим:
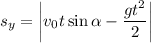
Подставляем значения:
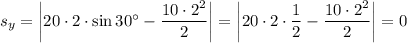
Зная проекции перемещения, найдем само перемещение:
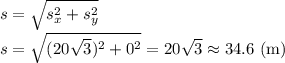
ответ: 34.6м
Разве, что рассматривать саму молекулу как осциллятор, когда её атомы колеблются относительно самой молекулы