Решение для тела, которое двигается по прямой без сил, то есть тормозит (ускорение отрицательное).
Нам понадобятся формулы:
1) Закон сохранения энергии механики:
E(в конце движения) = E(в начале движения) + Aтр (1)
2) Путь через начальную и конечную скорости и ускорение:
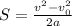 (2)
(2)
В начале, тело обладало энергией:
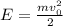 (3)
(3)
где v₀ - начальная скорость.
В конце, тело остановилось, то есть E = 0
Из закона (1) следует, что раз E(в конце движения) = 0, то вся энергия тела (3) ушла в Aтр. Обновлённая формула:
E = -Aтр. (4)
Aтр = Fтр * S (S - путь, который тело). По формуле (2):
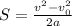
Но v = 0 (тело остановилось), следовательно:
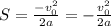
Минусы в (4) формуле и в этой сокращаются, и получается формула:
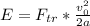
Подставляя (3) и выводя Fтр, получаем ответ:
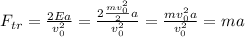
Начальная скорость не нужна.
Пусть V – полный объем льдины, x – объем подводной части льдины.
По закону Архимеда на тело, погруженное в жидкость, действует сила, равная весу жидкости в объеме погруженной части тела.
Объем погруженной части льдины – x куб. м.
Средняя плотность морской воды 1025 кг/куб. м.
Вес x куб. м. воды: P =1025xg
Этот вес, согласно третьему закону Ньютона, равен силе тяжести, действующей на льдину:
P = mg = pVg
где p = 916 кг/куб. м. - плотность льда (при 0 градусов). V – общий объем льдины.
Приравниваем обе силы
1025xg = 916Vg,
1025x = 916V
Тогда доля подводной части x/V от общего объема льдины V равна:
x/V = 916 / 1025 = 0,89
Тогда доля надводной части льдины равна:
1-x/V = 0,11 - то есть приблизительно одна десятая от полного объема льдины