Объяснение: s=107,5 м.
Будем считать движение автобуса при разгоне - равноускоренным, а при торможении - равнозамедленным. Пусть a1 - ускорение автобуса при разгоне и a2 - замедление автобуса при торможении. Так как при разгоне автобус увеличил свою скорость на Δv=18 км/ч=18/3,6=5 м/c за время Δt1=5 с, то a1=Δv/Δt1=5/5=1 м/с². При этом автобус путь s1=a1*(Δt1)²/2=1*25/2=12,5 м. При движении с постоянной скоростью автобус путь s2=(v0+Δv)*25 м, где v0 - начальная скорость автобуса. Так как по условию v0=0, то s2=Δv*25=5*25=75 м. При торможении скорость автобуса v=(v0+Δv)-a2*Δt2, где Δt2 - время торможения. Отсюда v=5-a2*8 м/с. Так как в момент остановки автобуса v=0, то из уравнения 5-8*a2=0 находим a2=5/8=0,625 м/с². При торможении автобус путь s3=(v0+Δv)*Δt2-a2*(Δt2)²/2=5*8-0,625*64/2=20 м. Отсюда полный путь s=s1+s2+s3=12,5+75+20=107,5 .
Объяснение:
Задача 1
V₀ = 36 км/ч = 10 м/м
V = 0
S = 62,5 см = 0,625 м
_________________________
n - ?
Из формулы:
S = (V²-V₀²) / (2·a)
Ускорение:
a = (V²-V₀²) / (2·S) = (0² - 10²)/(2·0,625) = - 80 м/с²
Ускорение отрицательное, поскольку происходило торможение.
Перегрузка (по модулю):
n = a / g = 80 / 10 = 8
Восьмикратная перегрузка.
Задача 2
m = 1,6 кг
k = 400 Н/м
μ = 0,3
___________
Δx - ?
Составим уравнение:
k·Δx = μ·m·g
Δx = μ·m·g / k = 0,3·1,6·10/40 = 0,12 м или 12 см
Задача 3
M = 150 г = 0,15 кг
d₁ = d/4
_____________
Mлин - ?
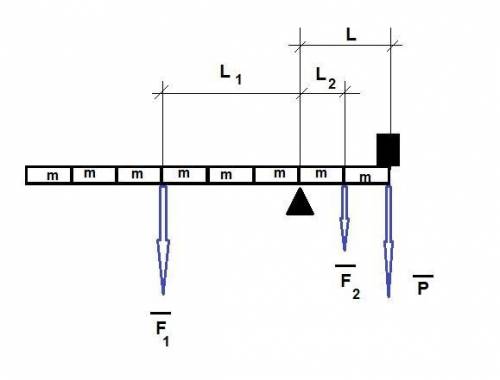
Сделаем чертеж.
Разделим линейку на 8 единичных частей.
Пусть масса 1 части равна m.
Составим условие равновесия:
F₁·L₁ = F₂·L₂+P·L
(6·m·g)·3 = (2·m·g)·1 + Mg·2
18m = 2·m + 0,150·2/g
16m = 3/10
m=3/160
Но масса всей линейки в 8 раз больше:
Mлинейки = 8·3/160 = 0,15 кг
Отсюда имеем уравнение:
Или
откуда и находится искомая температура