w = 2pi / T - циклическая частота маятника (измеряется в радианах)
T = 1/v => v = 1/T - период и частота колебаний маятника (период измеряется в секундах, а частота - в герцах)
Уравнение гармонических колебаний при условии, что наблюдения начали в момент, когда маятник был в положении равновесия:
x = A*sin(w*t), где
х - координата груза маятника в момент времени t
A - максимальная отклонение
w - циклическая частота
t - момент времени
Тогда:
Частота - это количество колебаний в секунду, значит:
v = 10/2 = 5/1 = 5 Гц
w = 2pi / T = 2pi * (1/T) = 2pi*v = 2pi*5 = 10pi
x = 5*sin(10pi*t) - уравнение гармонических колебаний, удовлетворяющее условиям задачи.
Объяснение:
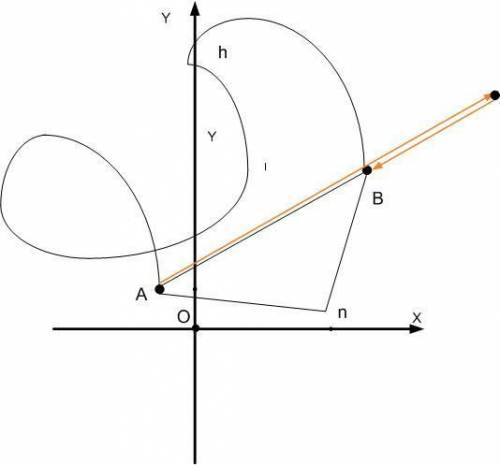
Материальная точка переместилась из т.А в т.В. Модуль перемещения равен кратчайшему расстоянию между двумя точками, т.е. длине отрезка l АВ l.
МТ могла перемещаться из т.А в т.В по различным траекториям. Могла по криволинейной АhB, могла по двум прямолинейным участка An - nB.
В обоих случаях путь, пройденный МТ будет больше l AB l. Значит, чтобы путь был равен перемещению МТ должна двигаться по прямой, проходящей через точки А и В, т.е. движение должно быть прямолинейным. Но МТ, двигаясь прямолинейно и по прямой, проходящей через АВ, может вначале переместиться в т.С, а затем вдоль той же прямой вернуться в т.В. Опять путь будет больше перемещения. Значит добавим еще одно ограничение: за все время движения направление вектора скорости не должно изменяться.
Т.е. ничего не мешает МТ двгаться неравномерно (с ускорением), когда модуль вектора скорости изменяется. Лишь бы не менялось направление вектора.
Маленькое замечание: все это верно для движения на плоскости и/или в пространстве, описываемыми геометрией Эвклида.
учитывая, что
сила
масса
время
скорость
работа
объем